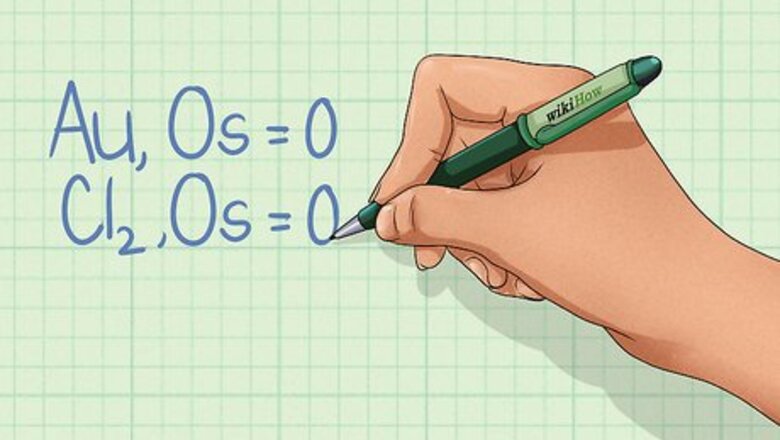
views
X
Research source
Reduction and oxidation refer to the transfer of electrons between elements or compounds and is designated by the oxidation state.[2]
X
Research source
An atom is oxidized when its oxidation number increases and is reduced when its oxidation number decreases. Redox reactions are essential to the basic functions of life such as photosynthesis and respiration.[3]
X
Research source
Balancing a redox reaction has a few more steps involved than balancing a regular chemical equation. The most important step is identifying whether or not a redox reaction is actually taking place.
Identifying a Redox Reaction
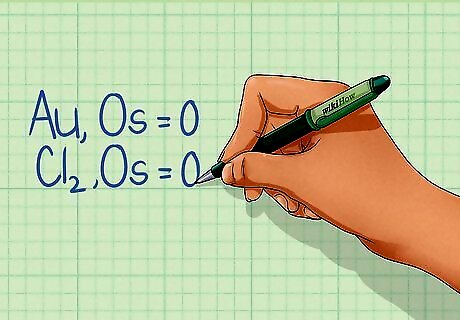
Learn the rules for assigning oxidation state. The oxidation state of a species (each element in the equation) is a number equal to the number of electrons that can be gained, lost, or shared with another element during the chemical bonding process. There are seven rules that allow you to determine the oxidation state of an element. They must be followed in the order given below. If two rules conflict, use the first rule to assign oxidation state (OS). Rule #1: An individual atom, by itself, has an OS of 0. For example: Au, OS = 0. Cl2 also has an OS of 0 as long as it is not combined with any other element. Rule #2: The total OS of all atoms in a neutral species is 0, but in an ion is equal to the ion charge. The molecule's OS must equal 0, but the OS for each element in that molecule may not be zero. For example, H2O has an OS of 0, but each hydrogen atom has an OS of +1, while the oxygen atom has an OS of -2. The ion Ca has an oxidation state of +2. Rule #3: For compounds, Group 1 metals have an OS of +1 and Group 2 metals have an OS +2. Rule #4: The oxidation state of fluorine in a compound is -1. Rule #5: The oxidation state of hydrogen in a compound is +1. Rule #6: The oxidation state of oxygen in a compound is -2. Rule #7: In compounds with two-elements where at least one is a metal, elements in Group 15 have an OS of -3, Group 16 have an OS of -2, and Group 17 have an OS of -1.
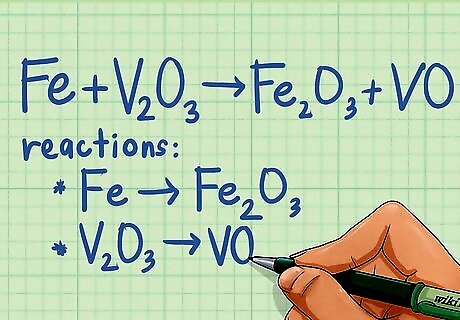
Split the reaction into two half-reactions. Although half-reactions are hypothetical reactions, splitting the equation allows you to easily determine whether a redox reaction is occurring. To do this, take the first reactant and write it as a half-reaction with the product that includes the element in the reactant. Then take the second reactant and write it as half-reaction with the product that includes that element. For example: Fe + V2O3 ---> Fe2O3 + VO breaks down into the following two half-reactions: Fe ---> Fe2O3 V2O3 ---> VO If there is only one reactant and two products, make one half-reaction with the reactant and the first product, and one half-reaction with the reactant and the second product. When combining the half-reactions at the end, don't forget to recombine the reactants. You can do the same if there are two reactants and only one product: use each reactant with the same product for the half-reactions. ClO ---> Cl + ClO3 Half-reaction 1: ClO ---> Cl Half-reaction 2: ClO ---> ClO3
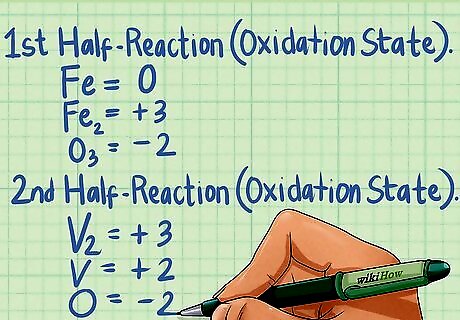
Assign oxidation states to each element in the equation. Using the seven rules for assigning oxidation states, determine the oxidation state for each species in the given chemical equation. Although a compound may be neutral, the elements that make up that compound will have a charged oxidation state. Remember to follow the rules in order. For the first half-reaction in our above example: OS for the Fe atom alone is 0 (rule #1), OS for the Fe in Fe2 is +3 (rule #2 and #6), and the OS for the O in O3 is -2 (rule #6). For the second half-reaction: OS for the V in V2 is +3 (rule #2 and #6) while OS for the O in O3 is -2 (rule #6). OS for V is +2 (rule #2), while O is -2 (rule #6).
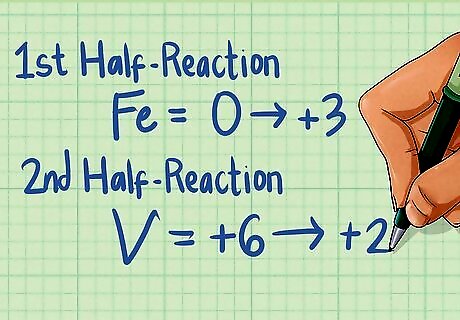
Determine if one species is oxidized and one is reduced. Looking at the oxidation states of each species in your half reaction, determine if one species is being oxidized (oxidation state increases), while the other species is reduced (oxidation state decreases). In our example, the first half-reaction is oxidized because Fe starts with an OS of 0 and goes up to 3. The second half-reaction is being reduced because V starts with an OS of +6 and goes down to +2. Because one species is oxidized and the other reduced, this equation is a redox reaction.
Balancing a Redox Reaction in a Neutral or Acidic Solution
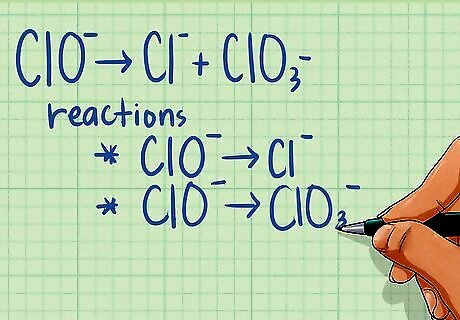
Split reaction into two half-reactions. Your equation should already be split into two half-reactions from the earlier step of determining whether or not a redox reaction was occurring. If you were already told it was a redox reaction, then your first step is to split it into two half-reactions. To do this, take the first reactant and write it as a half-reaction with the product that includes the element in the reactant. Then take the second reactant and write it as a half-reaction with the product that includes that element. For example: Fe + V2O3 ---> Fe2O3 + VO breaks down into the following two half-reactions: Fe ---> Fe2O3 V2O3 ---> VO If there is only one reactant and two products, make one half-reaction with the reactant and the first product, and one half-reaction with the reactant and the second product. When combining the half-reactions at the end, don't forget to recombine the reactants. You can do the same if there are two reactants and only one product: use each reactant with the same product for the half-reactions. ClO ---> Cl + ClO3 Half-reaction 1: ClO ---> Cl Half-reaction 2: ClO ---> ClO3
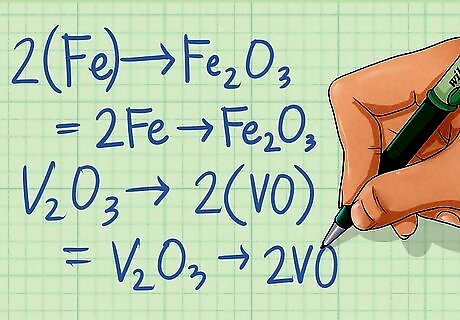
Balance all elements in the equation except hydrogen and oxygen. After you have determined that a redox reaction is occurring, it is time to balance it. Start by balancing all the elements in the each half-reaction that aren't hydrogen (H) or oxygen (O). These will be balanced in the following steps. Half-reaction 1: Fe ---> Fe2O3 There is 1 Fe atom on the left side and 2 on the right, multiply the left by 2 to balance. 2Fe ---> Fe2O3 Half-reaction 2: V2O3 ---> VO There are 2 V atoms on the left side and one on the right, multiply the right by 2 to balance. V2O3 ---> 2VO
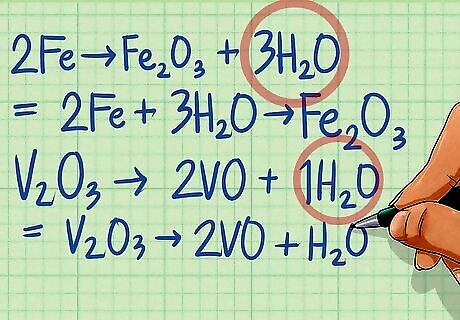
Balance the oxygen atoms by adding H2O to the opposite side of the reaction. Determine the number of oxygen atoms on each side of the equation. Balance the equation by adding water molecules to the side that has fewer oxygen atoms until both sides are equal. Half-reaction 1: 2Fe ---> Fe2O3 There are 3 O atoms on the right side and none on the left. Add 3 H2O molecules to the left side to balance. 2Fe + 3H2O ---> Fe2O3 Half-reaction 2: V2O3 ---> 2VO There are 3 O atoms on the left side and two on the right. Add 1 H2O molecule to the right side to balance. V2O3 ---> 2VO + H2O
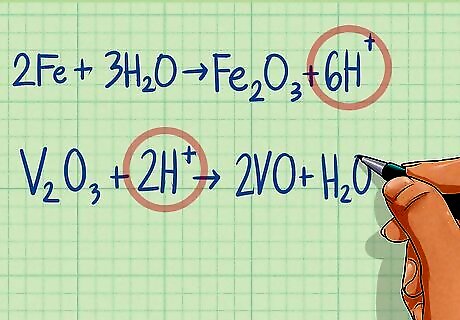
Balance hydrogen atoms by adding H to the opposite of the equation. Like you did with the oxygen atoms, determine the number of hydrogen atoms on each side of the equation. Then balance by adding H atoms to the side that has fewer atoms until both sides are equal. Half-reaction 1: 2Fe + 3H2O ---> Fe2O3 There are 6 H atoms on the left side and none on the right side. Add 6 H to the right side to balance. 2Fe + 3H2O ---> Fe2O3 + 6H Half-reaction 2: V2O3 ---> 2VO + H2O There are 2 H atoms on the right side and none on the left. Add 2 H to the left side to balance. V2O3 + 2H ---> 2VO + H2O
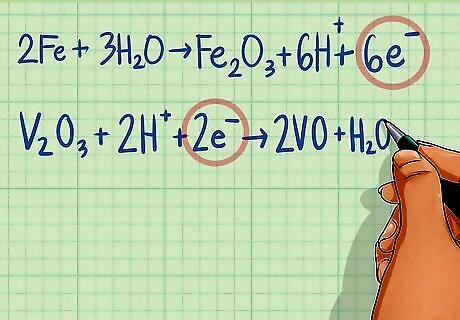
Equalize the charges by adding electrons to the proper side of the equation. After you have balanced the hydrogens and oxygens, one side of your equation will be more positive than the other. Add enough electrons to the side of each equation that is more positive to make the charge equal zero. Electrons will almost always be added to the side with the H atoms. Half-reaction 1: 2Fe + 3H2O ---> Fe2O3 + 6H The charge on the left side of the equation is 0 while the right side has a 6+ charge due to the hydrogen ions. Add 6 electrons to the right side to balance. 2Fe + 3H2O ---> Fe2O3 + 6H + 6e Half-reaction 2: V2O3 + 2H ---> 2VO + H2O The charge on the left side of the equation is 2+ while the right side is 0. Add 2 electrons to the left side to bring the charge to zero. V2O3 + 2H + 2e ---> 2VO + H2O
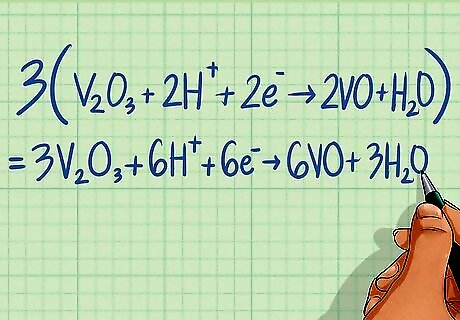
Multiply each half-reaction by a scaling factor so that the electrons are equal in both half-reactions. The electrons on either side of the equation must be made equal so when the half-reactions are added together, the electrons will cancel out. Multiply the reaction by the lowest common factor of the electrons to make them the same. Half-reaction 1 has 6 electrons while half-reaction 2 has 2 electrons. By multiplying half-reaction 2 by 3, it will have 6 electrons and be equal to the first half-reaction. Half-reaction 1: 2Fe + 3H2O ---> Fe2O3 + 6H + 6e Half-reaction 2: V2O3 + 2H + 2e ---> 2VO + H2O Multiply by 3: 3V2O3 + 6H + 6e ---> 6VO + 3H2O
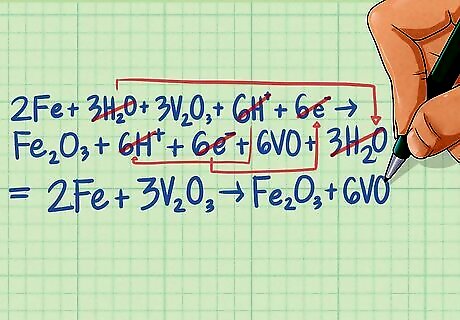
Combine the two half-reactions. Write all of the reactants on the left side of the equation and all of the products on the right side of the equation. You'll notice that there are like terms on each side including H2O, H and e. You can cancel out like terms, with the remaining terms leaving a balanced equation. 2Fe + 3H2O + 3V2O3 + 6H + 6e ---> Fe2O3 + 6H + 6e + 6VO + 3H2O The electrons on either side of the equation cancel out yielding: 2Fe + 3H2O + 3V2O3 + 6H ---> Fe2O3 + 6H + 6VO + 3H2O There are 3 H2O and 6 H ions on either side of the equation that also cancel yielding a final balanced equation: 2Fe + 3V2O3 ---> Fe2O3 + 6VO

Double-check that each side of your equation has the same charge. When you're done balancing, check to make sure that the charges are balanced on each side of the equation. The charges on each side of the equation should be the same. For the right side of our equation: OS for Fe is 0. In V2O3 the OS for V is +3 and for O is -2. Multiplying by the number of atoms of each element, V = +3 x 2 =6, O = -2 x 3 = -6. The charges cancel out. For the left side of our equation: In Fe2O3 the OS for Fe is +3 and for O is -2. Multiplying by the number of atoms of each element, Fe = +3 x 2 = +6, O = -2 x 3 = -6. The charges cancel out. In VO the OS for V is +2, while for O it's -2. The charges also cancel out on this side. Because all the charges equal zero, our equation has been correctly balanced.
Balancing a Redox Reaction in a Basic Solution
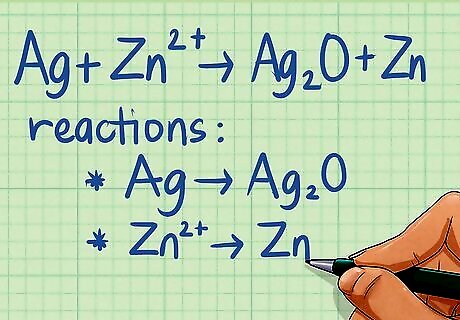
Split reaction into two half-reactions. Balancing in a basic solution follows the same steps as above, with one extra step at the end. Again, your equation should already be split into two half-reactions from the earlier step of determining whether or not a redox reaction was occurring. If you were already told it was a redox reaction, then your first step is to split it into two half-reactions. To do this, take the first reactant and write it as a half-reaction with the product that includes the element in the reactant. Then take the second reactant and write it as a half-reaction with the product that includes that element. For example, balance the following reaction in a basic solution: Ag + Zn ---> Ag2O + Zn breaks down into the following two half-reactions: Ag ---> Ag2O Zn ---> Zn
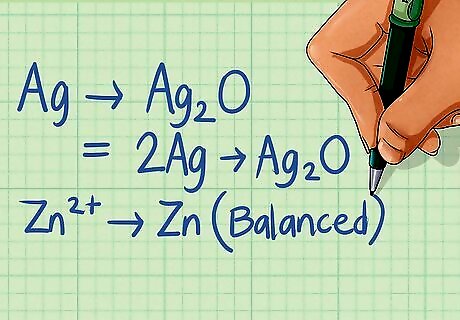
Balance all elements in the equation except hydrogen and oxygen. After you have determined that a redox reaction is occurring, it is time to balance it. Start by balancing all the elements in the each half-reaction that aren't hydrogen (H) or oxygen (O). These will be balanced in the following steps. Half-reaction 1: Ag ---> Ag2O There is 1 Ag atom on the left side and 2 on the right, multiply the left by 2 to balance. 2Ag ---> Ag2O Half-reaction 2: Zn ---> Zn There is 1 Zn atom on the left and 1 on the right, therefore it is already balanced.
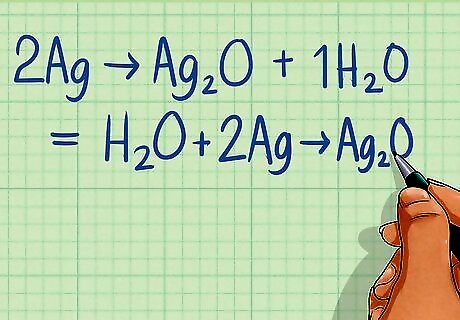
Balance the oxygen atoms by adding H2O to the opposite side of the reaction. Determine the number of oxygen atoms on each side of the equation. Balance the equation by adding water molecules to the side that has fewer oxygen atoms until both sides are equal. Half-reaction 1: 2Ag ---> Ag2O There are no O atoms on the left side and one on the right. Add 1 H2O molecule to the left side to balance. H2O + 2Ag ---> Ag2O Half-reaction 2: Zn ---> Zn There are no O atoms on either side, therefore it is balanced.
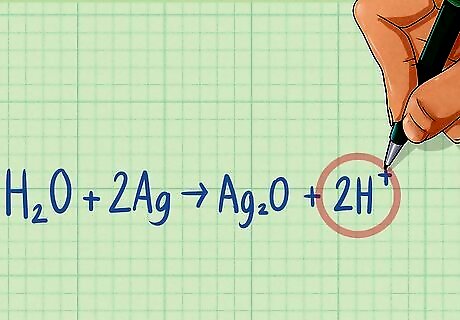
Balance hydrogen atoms by adding H to the opposite of the equation. Like you did with the oxygen atoms, determine the number of hydrogen atoms on each side of the equation. Then balance by adding H atoms to the side that has fewer atoms until both sides are equal. Half-reaction 1: H2O + 2Ag ---> Ag2O There are 2 H atoms on the left side and none on the right side. Add 2 H to the right side to balance. H2O + 2Ag ---> Ag2O + 2H Half-reaction 2: Zn ---> Zn There are no H atoms on either side, therefore it is balanced.
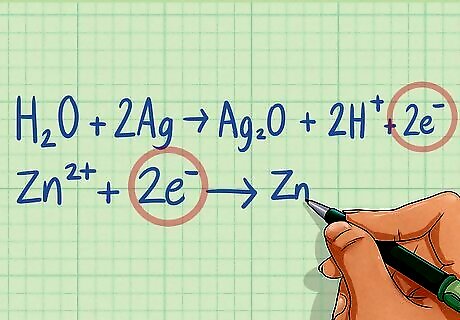
Equalize the charges by adding electrons to the proper side of the equation. After you have balanced the hydrogens and oxygens, one side of your equation will be more positive than the other. Add enough electrons to the side of each equation that is more positive to make the charge equal zero. Electrons will almost always be added to the side with the H atoms. Half-reaction 1: H2O + 2Ag ---> Ag2O + 2H The charge on the left side of the equation is 0 while the right side has a 2+ charge due to the hydrogen ions. Add 2 electrons to the right side to balance. H2O + 2Ag ---> Ag2O + 2H + 2e Half-reaction 2: Zn ---> Zn The charge on the left side of the equation is 2+ while the right side is 0. Add 2 electrons to the left side to bring the charge to zero. Zn + 2e ---> Zn
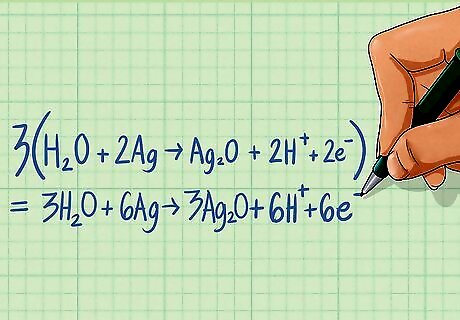
Multiply each half-reaction by a scaling factor so that the electrons are equal in both half-reactions. The electrons on either side of the equation must be made equal so when the half-reactions are added together, the electrons will cancel out. Multiply the reaction by the lowest common factor of the electrons to make them the same. For our example, both sides are already balanced with 2 electrons on each side.

Combine the two half-reactions. Write all of the reactants on the left side of the equation and all of the products on the right side of the equation. You'll notice that there are like terms on each side including H2O, H and e. You can cancel out like terms, with the remaining terms leaving a balanced equation. H2O + 2Ag + Zn + 2e ---> Ag2O + Zn + 2H + 2e The electrons on either side of the equation cancel out yielding: H2O + 2Ag + Zn ---> Ag2O + Zn + 2H
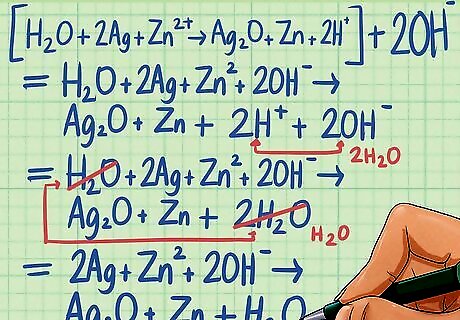
Balance the positive hydrogen ions with negative hydroxyl ions. Because you want to balance in a basic solution, you want to cancel out the hydrogen ions. Add an equal number OH ions to balance out the H ions. When adding OH ions, you must add the same number to both sides of the equation. H2O + 2Ag + Zn ---> Ag2O + Zn + 2H There are 2 H ions on the right side of the equation. Add 2 OH ions to both sides of the equation. H2O + 2Ag + Zn + 2OH ---> Ag2O + Zn + 2H + 2OH H and OH combine to form one water molecule (H2O), yielding H2O + 2Ag + Zn + 2OH ---> Ag2O + Zn + 2H2O You can cancel one water molecule on the right side, yielding a final balanced equation of: 2Ag + Zn + 2OH ---> Ag2O + Zn + H2O

Double-check that each side of your equation has zero charge. When you're done balancing, check to make sure that the charges are balanced on each side of the equation. The charges (oxidation state of all the elements) on each side of the equation should equal zero. For the left side of our equation: Ag has an OS of 0. The Zn For the right side: In Ag2O, the Ag has an OS of +1, while O is -2. Multiplying by the number of atoms Ag = +1 x 2 = +2, the -2 of O cancels out. The Zn has an OS of 0. The water molecule also has an OS of 0. Because all the charges equal zero, our equation has been correctly balanced.
















Comments
0 comment