
views
Understanding the PEMDAS Acronym

Learn the acronym. To do this, either remember the word “PEMDAS,” or you can remember the phrase “Please Excuse My Dear Aunt Sally.”

Understand the meaning of the acronym. P stands for “Parentheses”; E stands for “Exponents”; M stands for “Multiplication”; D stands for “Division”; A stands for “Addition”; and S stands for “Subtraction.”
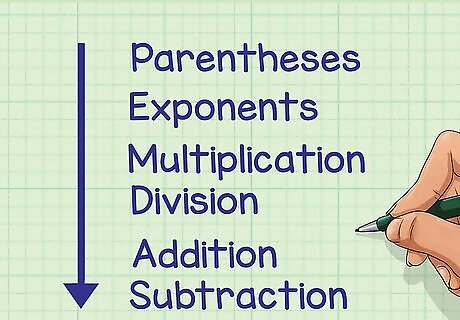
Understand the order of operations. The order of operations is the standard sequence in which you must perform operations in an expression that has more than one. PEMDAS tells you the order in which you must complete the operations. If you calculate an expression without using the order of operations, your answer will be incorrect.
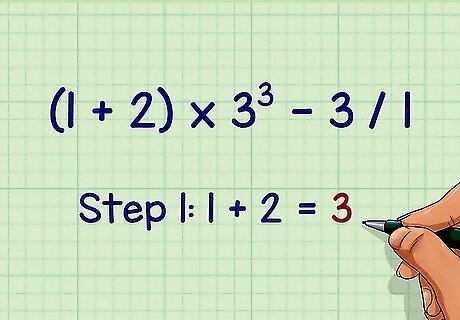
Calculate expressions in parentheses first. Not all problems will have them, so If you don’t see parentheses, you can skip this step.
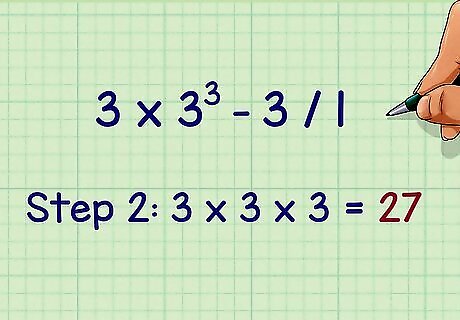
Calculate exponents second. If there are no exponents, skip this step.
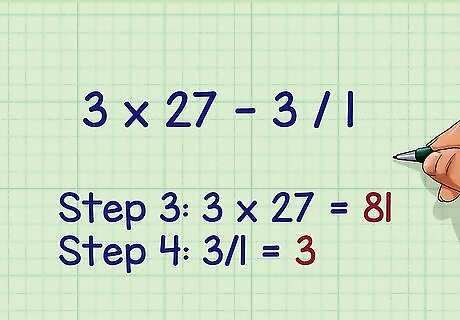
Multiply and divide third. These operations are of equal importance and must be performed from left to right. If there is no multiplication or division, skip this step.

Add and subtract fourth. These operations are of equal importance and must be performed from left to right. If there is no addition or subtraction, skip this step.
Applying the PEMDAS Acronym
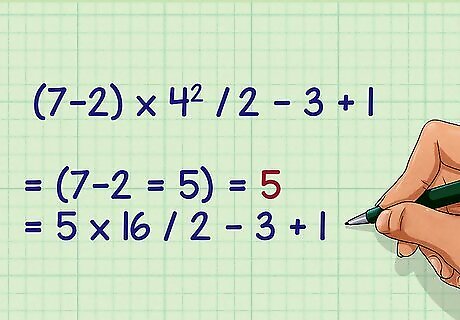
Check for parentheses. Any operations contained within parentheses must be completed first. For example, if you are solving ( 7 − 2 ) × 4 2 ÷ 2 − 3 + 1 {\displaystyle (7-2)\times 4^{2}\div 2-3+1} (7-2)\times 4^{{2}}\div 2-3+1, your first step is to calculate 7 − 2 = 5 {\displaystyle 7-2=5} 7-2=5. ( 7 − 2 ) × 4 2 ÷ 2 − 3 + 1 {\displaystyle (7-2)\times 4^{2}\div 2-3+1} (7-2)\times 4^{{2}}\div 2-3+1 = ( 5 ) × 4 2 ÷ 2 − 3 + 1 {\displaystyle =(5)\times 4^{2}\div 2-3+1} =(5)\times 4^{{2}}\div 2-3+1
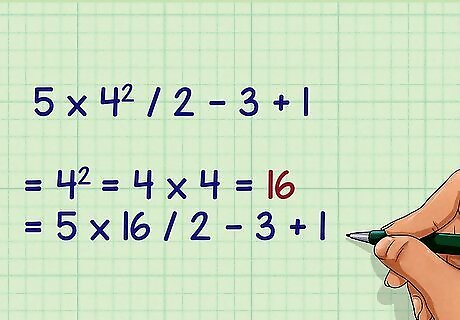
Check for Exponents. Calculate the value of all exponents in the expression. For example, the next step in 5 × 4 2 ÷ 2 − 3 + 1 {\displaystyle 5\times 4^{2}\div 2-3+1} 5\times 4^{{2}}\div 2-3+1 is to calculate 4 2 = 16 {\displaystyle 4^{2}=16} 4^{{2}}=16. 5 × 4 2 ÷ 2 − 3 + 1 {\displaystyle 5\times 4^{2}\div 2-3+1} 5\times 4^{{2}}\div 2-3+1 = 5 × 16 ÷ 2 − 3 + 1 {\displaystyle =5\times 16\div 2-3+1} =5\times 16\div 2-3+1
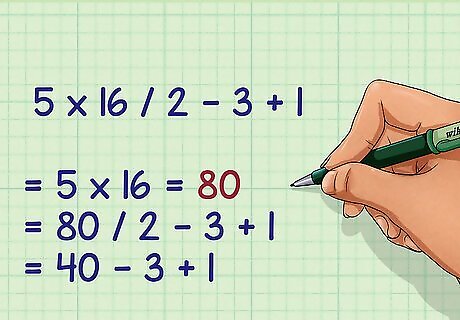
Check for multiplication and division. Remember, these two operations are equally important and should be completed left to right. For example, the next step in 5 × 16 ÷ 2 − 3 + 1 {\displaystyle 5\times 16\div 2-3+1} 5\times 16\div 2-3+1 is to calculate 5 × 16 = 80 {\displaystyle 5\times 16=80} 5\times 16=80. Then you would complete the division. Thus: 5 × 16 ÷ 2 − 3 + 1 {\displaystyle 5\times 16\div 2-3+1} 5\times 16\div 2-3+1 = 80 ÷ 2 − 3 + 1 {\displaystyle =80\div 2-3+1} =80\div 2-3+1 = 40 − 3 + 1 {\displaystyle =40-3+1} =40-3+1
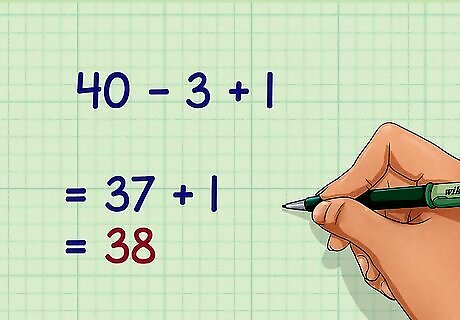
Check for addition and subtraction. These two operations are also equally important and should be completed left to right. For example, the next step in 40 − 3 + 1 {\displaystyle 40-3+1} 40-3+1 is to calculate 40 − 3 = 37 {\displaystyle 40-3=37} 40-3=37. Then you would complete the addition. Thus: 40 − 3 + 1 {\displaystyle 40-3+1} 40-3+1 = 37 + 1 {\displaystyle =37+1} =37+1 = 38 {\displaystyle =38} =38
















Comments
0 comment