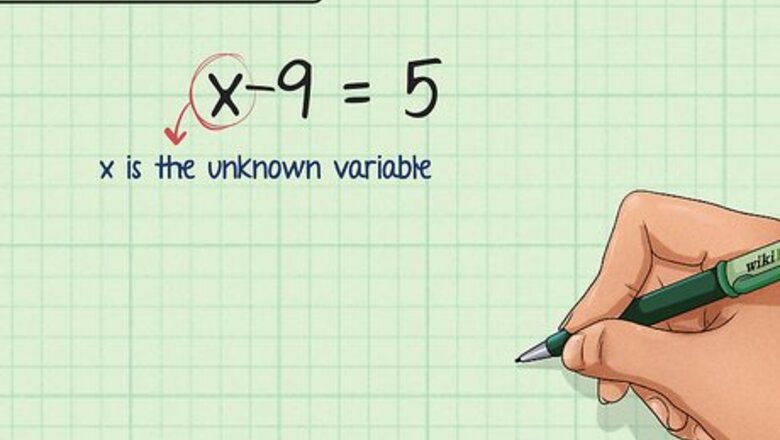
views
X
Research source
In algebra, you'll often work with equations that have an unknown value represented by a variable, or letter. To solve these equations, you need to find the value of the variable. A one-step equation is one in which you only have to perform just one operation to determine the unknown value, and so these type of equations are the easiest to solve. We'll show you how!
- Write down your equation and identify how to "isolate" the variable, to get it alone one side of the equals sign.
- Add or subtract the constant that's on the same side of the equals sign as the variable from both sides of the equation.
- Or, multiply or divide the constant if the equation uses multiplication or division.
Adding or Subtracting to Solve

Write down the equation. It’s easy to solve equations when you understand what they mean. An equation will have a variable (usually x {\displaystyle x} x), which represents an unknown value. The equation will also have a constant, which is a number you need to add or subtract from the variable to equal a certain sum or difference. For example, you might have the equation x − 9 = 5 {\displaystyle x-9=5} x-9=5. The variable representing the unknown number is x {\displaystyle x} x. When you subtract 9 from the unknown number, the difference is 5.
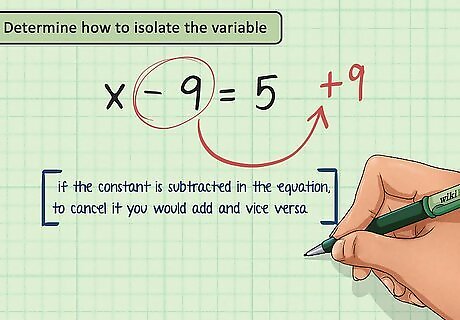
Determine how to isolate the variable. To isolate a variable, you need to get it alone on one side of the equation by performing an inverse operation to cancel the constants. Addition and subtraction are inverse operations. So, if the constant is subtracted in the equation, to cancel it you would add. For example, in the equation x − 9 = 5 {\displaystyle x-9=5} x-9=5, 9 is subtracted from the variable, so to isolate the variable you must cancel the 9 by adding it.
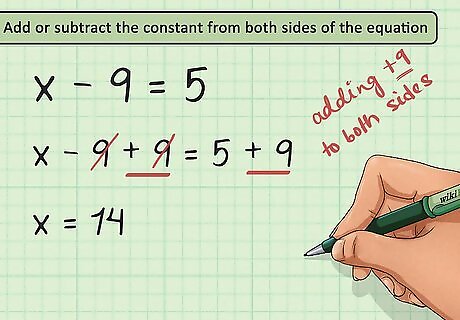
Add or subtract the constant from both sides of the equation. As you manipulate equations to solve them, you must keep both sides balanced. Whatever you do to one side of the equation, you must do to the other side. So, if you need to add a value to isolate the variable, you must also add that same value to the other side of the equation. For example, in the equation x − 9 = 5 {\displaystyle x-9=5} x-9=5, you need to add 9 to the left side to isolate the variable, so you also need to add 9 to the right side of the equation: x − 9 = 5 {\displaystyle x-9=5} x-9=5 x − 9 + 9 = 5 + 9 {\displaystyle x-9+9=5+9} x-9+9=5+9 x = 14 {\displaystyle x=14} x=14.

Check your work. To make sure your solution is correct, plug the value of x {\displaystyle x} x into the original equation. If the equation is true, your solution is correct. For example, if you found that x = 14 {\displaystyle x=14} x=14, substitute 14 for x {\displaystyle x} x in the original equation: 14 − 9 = 5 {\displaystyle 14-9=5} 14-9=5. Since this equation is true, your solution is correct.
Dividing or Multiplying to Solve

Evaluate the equation. The variable, usually x {\displaystyle x} x, represents an unknown value. Solving an equation means finding the unknown value. The equation may also have a coefficient, which is a number you need to multiply by the variable to equal a certain product. The variable may also be the numerator of a fraction. This means you need to divide the variable by the number in the denominator to equal a certain quotient. For example, you might have the equation 3 x = 24 {\displaystyle 3x=24} 3x=24. The variable representing the unknown number is x {\displaystyle x} x. When you multiply the unknown number and 3, the product is 24.
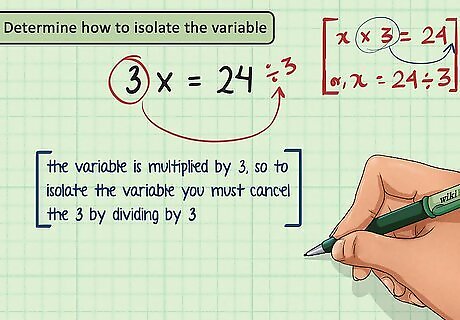
Determine how to isolate the variable. Isolating a variable means getting it by itself on one side of the equation. To do this you must perform an inverse operation to cancel coefficients or fractions. Multiplication and division are inverse operations. If the variable has a coefficient, to cancel it you would divide by the coefficient, since any number divided by itself is equal to 1. If the variable is the numerator of a fraction, to isolate it you would multiply by the denominator, since multiplying by a number cancels the division by that number. For example, in the equation 3 x = 24 {\displaystyle 3x=24} 3x=24 the variable is multiplied by 3, so to isolate the variable you must cancel the 3 by dividing by 3.

Multiply or divide from both sides of the equation. As you solve an equation the most important thing to remember is that you must keep both sides of the equation balanced. This means that whatever you do to one side of the equation, you must do to the other side, too. So, if you need to divide by a value to isolate the variable, you must also divide by the same value on the other side of the equation. For example, in the equation 3 x = 24 {\displaystyle 3x=24} 3x=24, you need to divide by 3 on the left side to isolate the variable, so you also need to divide by 3 on the right side of the equation: 3 x = 24 {\displaystyle 3x=24} 3x=24 3 x 3 = 24 3 {\displaystyle {\frac {3x}{3}}={\frac {24}{3}}} {\frac {3x}{3}}={\frac {24}{3}} x = 8 {\displaystyle x=8} x=8

Check your solution. To make sure your answer is correct, plug the value of x {\displaystyle x} x into the original equation. If the equation is true, your solution is correct. For example, if you found that x = 8 {\displaystyle x=8} x=8, substitute 8 for x {\displaystyle x} x in the original equation: 3 ( 8 ) = 24 {\displaystyle 3(8)=24} 3(8)=24. Since this equation is true, your solution is correct.
Completing Sample Problems

Solve this equation with a fraction: x 4 = 8 {\displaystyle {\frac {x}{4}}=8} {\frac {x}{4}}=8. Since the variable is divided by 4, to isolate it you need to multiply by 4. x 4 = 8 {\displaystyle {\frac {x}{4}}=8} {\frac {x}{4}}=8 4 ( x 4 ) = ( 4 ) 8 {\displaystyle 4({\frac {x}{4}})=(4)8} 4({\frac {x}{4}})=(4)8 x = 32 {\displaystyle x=32} x=32 Checking your work, since 32 4 = 8 {\displaystyle {\frac {32}{4}}=8} {\frac {32}{4}}=8, your solution is correct.

Solve this equation with a negative constant: − 16 + x = 29 {\displaystyle -16+x=29} -16+x=29. Since the constant is negative, adding it to both sides will isolate the variable. − 16 + x = 29 {\displaystyle -16+x=29} -16+x=29 − 16 + x + 16 = 29 + 16 {\displaystyle -16+x+16=29+16} -16+x+16=29+16 x = 45 {\displaystyle x=45} x=45 Checking your work, since − 16 + 45 = 29 {\displaystyle -16+45=29} -16+45=29, your solution is correct.

Solve this equation with a negative coefficient: − 5 x = 45 {\displaystyle -5x=45} -5x=45. Since the variable is multiplied by -5, to isolate the variable, you must divide each side by -5. Remember that dividing a positive number by a negative number equals a negative quotient. − 5 x = 45 {\displaystyle -5x=45} -5x=45 − 5 x − 5 = 45 − 5 {\displaystyle {\frac {-5x}{-5}}={\frac {45}{-5}}} {\frac {-5x}{-5}}={\frac {45}{-5}} x = − 9 {\displaystyle x=-9} x=-9 Checking your work, since − 5 ( − 9 ) = 45 {\displaystyle -5(-9)=45} -5(-9)=45, your solution is correct.















Comments
0 comment