How to Sum the Integers from 1 to N (What Formula to Use)

Finding the Sum of Consecutive Integers

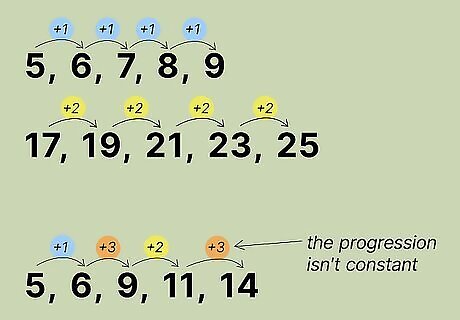
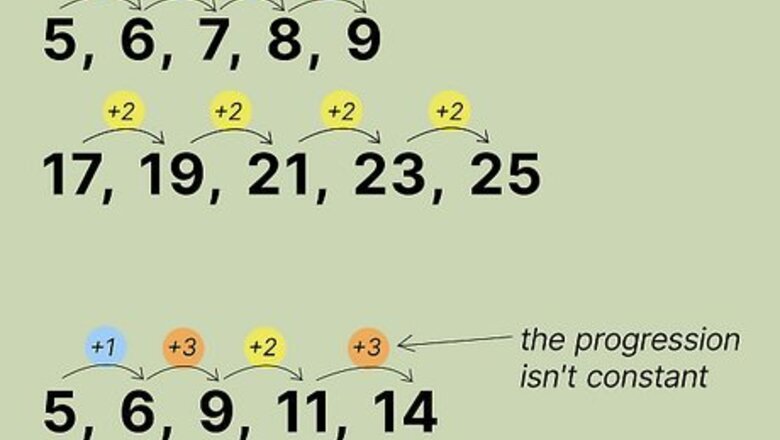
Identify the arithmetic sequence. Look at the range of numbers you're trying to add together. If you'd like to use a formula to sum the integers, ensure that the numbers progress in a constant amount. For example, 5, 6, 7, 8, 9 is a series, and so is 17, 19, 21, 23, 25. You couldn't use 5, 6, 9, 11, 14 because the progression isn't constant.

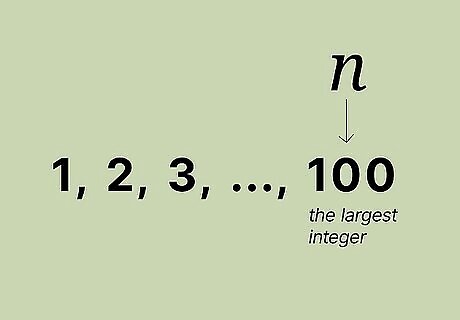
Define n {\displaystyle n} n for your sequence. To use a formula to find the sum of 1 to n {\displaystyle n} n, choose the largest integer to be n {\displaystyle n} n. For example, if you try adding all the integers from 1 to 100, n {\displaystyle n} n will be 100 because it's the largest integer in the sequence. As a reminder, integers are whole numbers, so n {\displaystyle n} n cannot be a decimal, fraction, or negative number.

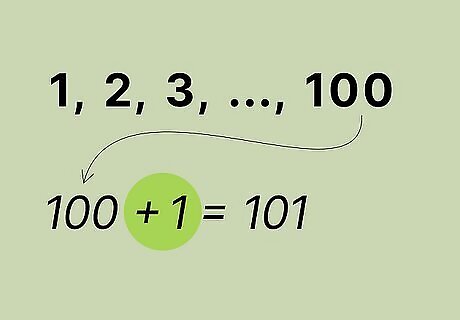
Identify how many integers you're adding. To sum the integers from your starting number to n {\displaystyle n} n, determine how many terms you add. For example, if you're adding the first 200 integers, you'll have 200 plus 1 to equal 201 integers. If you're adding the first integers from 1 to 12, you'll have 12 plus 1 to equal 13 terms.

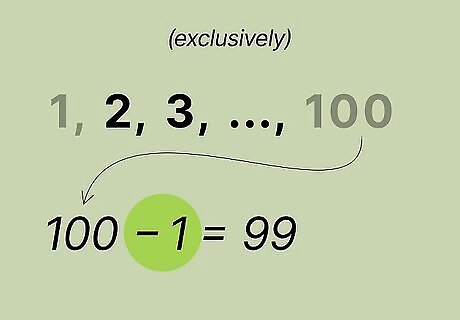
Decide if you're adding exclusively. You may be asked to find the sum of a range of integers between two integers. If you're summing exclusively, you'll need to subtract 1 from your n {\displaystyle n} n. For example, if you're finding the sum of the integers from 1 to 100 exclusively, subtract 1 from 100 to get 99.

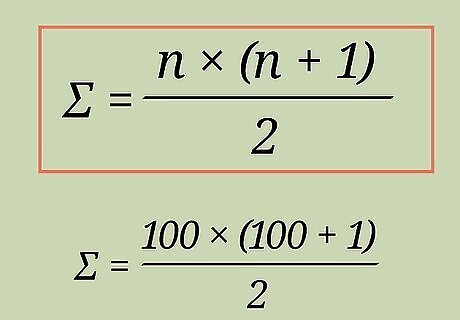
Define your formula for consecutive integers. Once you've defined n {\displaystyle n} n as the largest integer you're adding, plug the number into the formula to sum consecutive integers: sum = n {\displaystyle n} n∗( n {\displaystyle n} n+1)/2. For example, if you're summing the first 100 integers, plug 100 into n {\displaystyle n} n to get 100∗(100+1)/2. If you're finding the first 20 integers, use 20 for n {\displaystyle n} n. Work 20∗(20+1)/2 to get 420/2. Your answer will be 210.

Finding the Sum of Other Integers

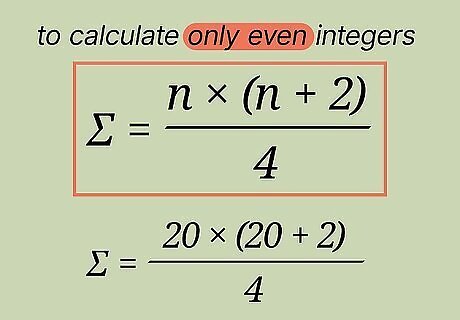
Set up a formula to calculate only even integers. If the problem asks you to find the sum of only the even integers in a sequence starting with 1, you'll need to use a different formula. Plug your highest integer into n {\displaystyle n} n so: sum = n {\displaystyle n} n∗( n {\displaystyle n} n+2)/4. For example, if the problem asks you to find the sum of even integers from 1 to 20, use 20 as n {\displaystyle n} n. Your formula will be 20∗22/4.

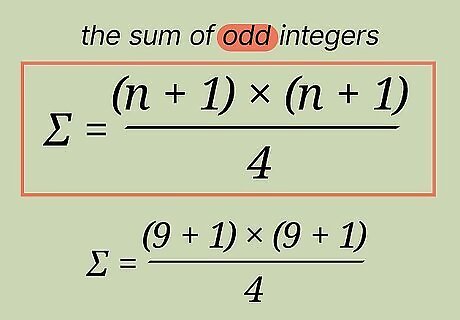
Define a formula to find the sum of odd integers. If the problem asks you to find the sum of only the odd integers, you'll need to find n {\displaystyle n} n first. To find n {\displaystyle n} n, add 1 to the highest number of the sequence. Then use it in this formula: sum = ( n {\displaystyle n} n+1)∗( n {\displaystyle n} n+1)/4. For example, to add the odd integers from 1 to 9, add 1 to 9. The equation will now look like 10∗(10)/4. Once you've worked the equation, you'll get 10∗(10)/4 to equal 25.