views
Decompose the following function in terms of its Fourier series. Generally speaking, we may find the Fourier series of any (piecewise continuous - see the tips) function on a finite interval. If the function is periodic, then the behavior of the function in that interval allows us to find the Fourier series of the function on the entire domain. f ( x ) = x 2 − 2 x + 1 : [ − 1 , 1 ] {\displaystyle f(x)=x^{2}-2x+1:\ [-1,1]} f(x)=x^{{2}}-2x+1:\ [-1,1]
Identify the even and odd parts of the function. Every function may be decomposed into a linear combination of even and odd functions. The Fourier basis is convenient for us in that this series already separates these components. Therefore, by careful observation of which parts of the function are even and which are odd, we can do the integrals separately knowing which terms vanish and which do not. For our function, x 2 + 1 {\displaystyle x^{2}+1} x^{{2}}+1 is even and − 2 x {\displaystyle -2x} -2x is odd. This means that b n = 0 {\displaystyle b_{n}=0} b_{{n}}=0 for x 2 + 1 {\displaystyle x^{2}+1} x^{{2}}+1 and a n = 0 {\displaystyle a_{n}=0} a_{{n}}=0 for − 2 x . {\displaystyle -2x.} -2x.
Evaluate the constant term. The constant term a 0 {\displaystyle a_{0}} a_{{0}} is actually the cos 0 π x L = 1 {\displaystyle \cos {\frac {0\pi x}{L}}=1} \cos {\frac {0\pi x}{L}}=1 term of the cosines. Note that − 2 x {\displaystyle -2x} -2x does not contribute to the integral because any constant function is even. a 0 = ∫ − 1 1 ( x 2 + 1 ) d x = 8 3 {\displaystyle a_{0}=\int _{-1}^{1}(x^{2}+1)\mathrm {d} x={\frac {8}{3}}} a_{{0}}=\int _{{-1}}^{{1}}(x^{{2}}+1){\mathrm {d}}x={\frac {8}{3}}
Evaluate the Fourier coefficients. Here, we may evaluate by way of integration by parts. It is useful to recognize that cos n π = ( − 1 ) n {\displaystyle \cos n\pi =(-1)^{n}} \cos n\pi =(-1)^{{n}} and sin n π = 0. {\displaystyle \sin n\pi =0.} \sin n\pi =0. It is also worth noting that the integral of a trigonometric function over one period vanishes. a n = ∫ − 1 1 ( x 2 + 1 ) cos n π x d x = 4 ( − 1 ) n n 2 π 2 {\displaystyle a_{n}=\int _{-1}^{1}(x^{2}+1)\cos n\pi x\mathrm {d} x={\frac {4(-1)^{n}}{n^{2}\pi ^{2}}}} a_{{n}}=\int _{{-1}}^{{1}}(x^{{2}}+1)\cos n\pi x{\mathrm {d}}x={\frac {4(-1)^{{n}}}{n^{{2}}\pi ^{{2}}}} b n = ∫ − 1 1 − 2 x sin n π x d x = 4 ( − 1 ) n n π {\displaystyle b_{n}=\int _{-1}^{1}-2x\sin n\pi x\mathrm {d} x={\frac {4(-1)^{n}}{n\pi }}} b_{{n}}=\int _{{-1}}^{{1}}-2x\sin n\pi x{\mathrm {d}}x={\frac {4(-1)^{{n}}}{n\pi }}
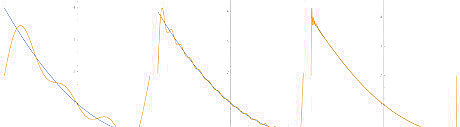
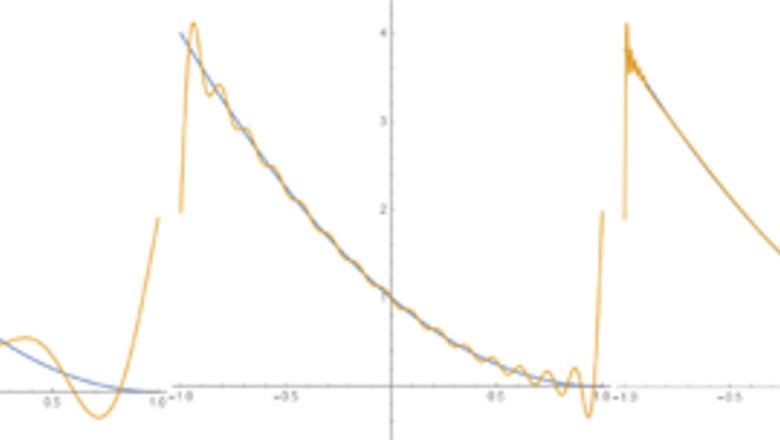
Write out the function in terms of its Fourier series. This series converges on the interval ( − 1 , 1 ) . {\displaystyle (-1,1).} (-1,1). Because the function is not periodic, the series does not hold on the whole interval, but rather in the neighborhood of any interior point (point-wise convergence as opposed to uniform convergence). x 2 − 2 x + 1 = 4 3 + ∑ n = 1 ∞ [ 4 ( − 1 ) n n 2 π 2 cos n π x + 4 ( − 1 ) n n π sin n π x ] {\displaystyle x^{2}-2x+1={\frac {4}{3}}+\sum _{n=1}^{\infty }\left[{\frac {4(-1)^{n}}{n^{2}\pi ^{2}}}\cos n\pi x+{\frac {4(-1)^{n}}{n\pi }}\sin n\pi x\right]} x^{{2}}-2x+1={\frac {4}{3}}+\sum _{{n=1}}^{{\infty }}\left[{\frac {4(-1)^{{n}}}{n^{{2}}\pi ^{{2}}}}\cos n\pi x+{\frac {4(-1)^{{n}}}{n\pi }}\sin n\pi x\right] The image shows the Fourier series up to n = 3 , {\displaystyle n=3,} n=3, n = 15 , {\displaystyle n=15,} n=15, and n = 100. {\displaystyle n=100.} n=100. We can clearly see the convergence here, as well as the overshoots near the boundaries that do not seem to vanish at higher n . {\displaystyle n.} n. This is the Gibbs phenomenon, which is the result of the failure of the series to converge uniformly on the prescribed interval.



















Comments
0 comment