views
Setting Up a Table
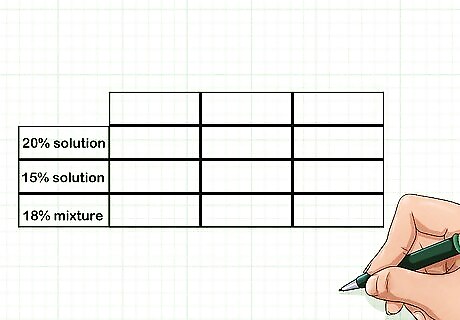
Create a table with three rows and three columns. The table will help you approach the problem logically so that you can set up an equation. The rows will represent each ingredient in the mixture, plus the mixture. So, for a mixture of two ingredients, you need three rows. Label the first row for ingredient 1, the second row for ingredient 2, and the third row for the mixture. For example, you might have a 20% saline solution, and a 15% saline solution. If you need to make 5 liters of an 18% saline solution, how many liters of each solution do you need to combine? For this problem you would label the three rows “20% solution,” “15% solution,” and “18% Mixture.”
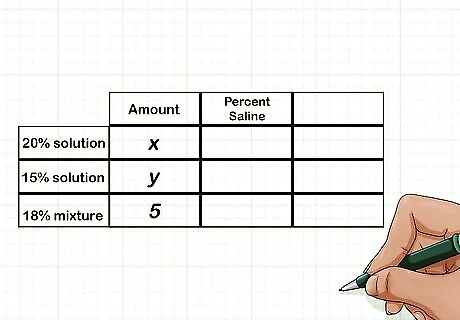
Label and fill in the first column. The first column will include values that represent the part of the total mixture or solution each ingredient is. Label the column “Amount” and fill in the cell for each ingredient. If the amount of each ingredient in the final mixture is unknown, use variables to represent these values. For example, if you are mixing saline solutions, you would label the column “Amount.” Since you don’t know how much of the 20% solution is in the final mixture, write the variable x {\displaystyle x} x in this cell. Since you also don’t know how much of the 15% solution is in the final mixture, write the variable y {\displaystyle y} y in this cell. Since you know that you need 5 liters of the final mixture, in this cell you will write 5.

Label and complete the second column. If you are completing a problem regarding diluted solutions, such as a saline solution, then this column will represent the percentage of saline in each unit of the ingredient. For example, you would label the second column “Percent Saline.” Since the first ingredient is 20% saline, in the first row you will write .20. Since the second solution is 15% saline, in the second row you will write .15. Since the final mixture needs to be 18% saline, in the third row you will write .18.
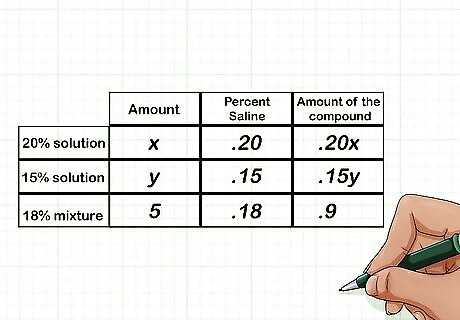
Label and complete the third column. If you are completing a problem regarding a diluted solution, then this column will represent the amount of the compound each ingredient adds to the total solution. To find the values for this column, multiply the first two values in each row. For example, you need x {\displaystyle x} x amount of the first ingredient, which is 20% saline, in the third column the value for this ingredient is .20 x {\displaystyle .20x} .20x. Since you need y {\displaystyle y} y amount of the second ingredient, which is 15% saline, in the third column the value for this ingredient is .15 y {\displaystyle .15y} .15y. For the total mixture, since you need 5 liters, and the salinity will be 18%, the value for the third column is ( 5 ) ( .18 ) = .9 {\displaystyle (5)(.18)=.9} (5)(.18)=.9, which means there is .9 {\displaystyle .9} .9 liters of saline in the final mixture.
Setting Up an Equation
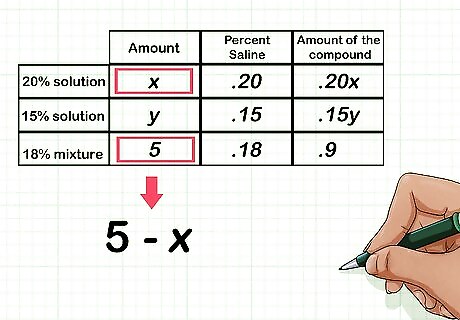
Rewrite the second variable in terms of x {\displaystyle x} x. Since you need to solve an equation, you should only be working with one variable. To rewrite the second variable, look at the total amount of the final mixture (the first column of your table). The difference between the total amount of the mixture and the first variable is equal to the second variable. For example, since you need 5 liters of the final mixture, and the first ingredient is equal to x {\displaystyle x} x liters of that solution, the second ingredient is equal to 5 − x {\displaystyle 5-x} 5-x liters.

Substitute the new expression of the second variable into the grid. Each time you see a y {\displaystyle y} y in the grid, replace the variable rewritten in terms of the x {\displaystyle x} x. Likely this will be in the second row, third column. For example, if you found that y = 5 − x {\displaystyle y=5-x} y=5-x, in the third column of the second ingredient, you need to change .15 y {\displaystyle .15y} .15y to .15 ( 5 − x ) {\displaystyle .15(5-x)} .15(5-x).

Write down the value in the third row of the third column. This is the total amount of the ingredient in the final mixture. This value will be the first half of your equation. For example, you know that the final 18% mixture will have .9 liters of saline in it. So the first half of your equation is .9 {\displaystyle .9} .9.

Add together the values in the first and second rows of the third column. These are the total amount of the compound each ingredient adds to the mixture. These addends are the second half of the equation. For example, since the final mixture will derive .20 x {\displaystyle .20x} .20x saline from the first ingredient, and .15 ( 5 − x ) {\displaystyle .15(5-x)} .15(5-x) saline from the second ingredient, your equation will look like this: .9 = .20 x + .15 ( 5 − x ) {\displaystyle .9=.20x+.15(5-x)} .9=.20x+.15(5-x).
Solving the Problem
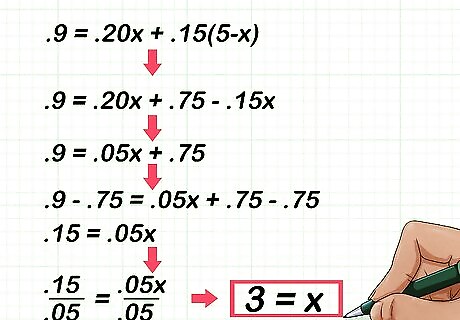
Solve the equation for x {\displaystyle x} x. Use the regular rules of algebra to isolate the variable. Remember that whatever you do to one side of the equation, you must also do to the other side. For example, to solve .9 = .20 x + .15 ( 5 − x ) {\displaystyle .9=.20x+.15(5-x)} .9=.20x+.15(5-x): First use the distributive property to simplify the value in parentheses: .9 = .20 x + .75 − .15 x {\displaystyle .9=.20x+.75-.15x} .9=.20x+.75-.15x. Second, combine the x {\displaystyle x} x terms: .9 = .05 x + .75 {\displaystyle .9=.05x+.75} .9=.05x+.75. Third, subtract .75 {\displaystyle .75} .75 from each side: .9 − .75 = .05 x + .75 − .75 {\displaystyle .9-.75=.05x+.75-.75} .9-.75=.05x+.75-.75 .15 = .05 x {\displaystyle .15=.05x} .15=.05x. Fourth, divide each side by .05 {\displaystyle .05} .05: .15 .05 = .05 x .05 {\displaystyle {\frac {.15}{.05}}={\frac {.05x}{.05}}} {\frac {.15}{.05}}={\frac {.05x}{.05}} 3 = x {\displaystyle 3=x} 3=xSo, you need 3 liters of the first ingredient, the 20% saline solution, for your final mixture.
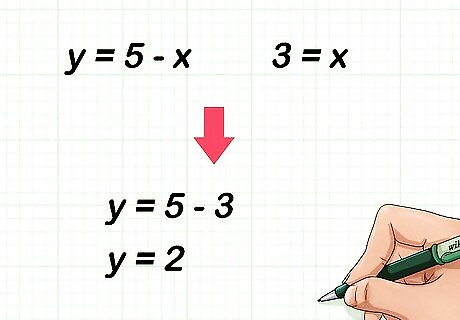
Find the value of y {\displaystyle y} y. Remember that in your original table you had two variables, x {\displaystyle x} x and y {\displaystyle y} y. To find the value of y {\displaystyle y} y, go back to the expression you used to restate y {\displaystyle y} y in terms of x {\displaystyle x} x. Plug the value of x {\displaystyle x} x into this equation and solve. For example, if you found that y = 5 − x {\displaystyle y=5-x} y=5-x and 3 = x {\displaystyle 3=x} 3=x, plug 3 into the equation and solve: y = 5 − 3 {\displaystyle y=5-3} y=5-3 y = 2 {\displaystyle y=2} y=2

Write out your final answer. The variable x {\displaystyle x} x will give you the missing value for the first ingredient. The variable y {\displaystyle y} y will give you the missing value for the second ingredient. For example, if you needed to find how many liters of a 20% saline solution and how many liters of a 15% saline solution you need combine to make 5 liters of a 18% solution, then x {\displaystyle x} x will tell you how many liters of the first solution you need, and y {\displaystyle y} y will tell you how many liters of the second solution you need. So if x = 3 {\displaystyle x=3} x=3 and y = 2 {\displaystyle y=2} y=2, you need 3 liters of the 20% solution, and 2 liters of the 18% solution.
Applying the Concept to Price Problems

Determine the two “ingredients.” These will be two items that are being combined. They might be food ingredients, or differently priced items, such as tickets. For example, you might be trying to solve the following problem: The student council is selling 100 cups of punch at a school dance. The punch is made from a combination of fruit juice and lemon-lime soda. They want to sell each cup of punch for $1.00. Normally they would sell a cup of fruit juice for $1.15 and a cup of lemon lime soda for $0.75. How many cups of each ingredient should the student council use to make the punch? In this problem, fruit juice and lemon-lime soda are the two ingredients.
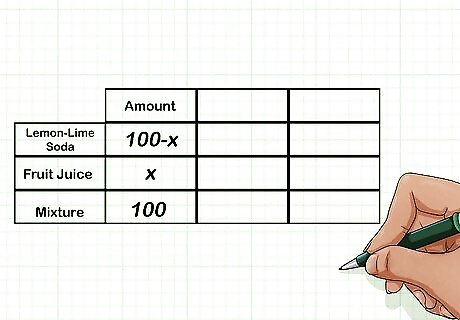
Fill out the first column of your chart. The first column will be the amount of each ingredient in the final mixture, and the total amount of the mixture. You will likely need to use variables. For example, since you know the student council plans on making 100 cups of punch, you would write 100 in the third row of the first column. For the fruit juice, you would write the variable x {\displaystyle x} x, since you don’t know how much fruit juice will be in the final mixture. For the lemon-lime soda, you would write 100 − x {\displaystyle 100-x} 100-x, since the amount will be the difference between the amount of the total mixture and the amount of the other ingredient.

Fill out the second column of your chart. This will be the unit price of each ingredient in the mixture, and the unit price of the mixture. For example, you know that the punch will be sold for $1.00 per cup, so write a 1 in the second column for the mixture. The fruit juice sells for $1.15 per cup, so write 1.15 in the second column for this ingredient. The soda sells for $0.75 per cup, so write 0.75 in the second column for lemon-lime soda.
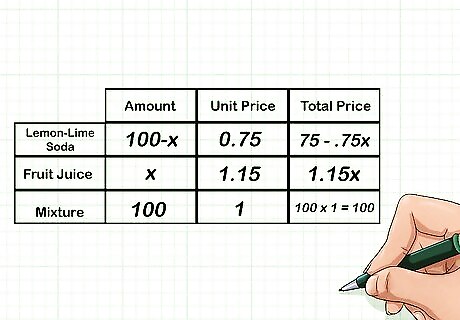
Fill out the third column of your chart. This column will represent the total price of each ingredient in the total mixture, as well as the total price of the mixture. To calculate this, multiply the values in the first and second column for each ingredient. For example, since 100 cups of punch will be made, and each cup will cost $1.00, the total price of the punch is 100 × 1 = 100 {\displaystyle 100\times 1=100} 100\times 1=100. Since there are x {\displaystyle x} x cups of fruit juice in the punch, and fruit juice is priced at $1.15 per cup, the total price of the fruit juice in the mixture is 1.15 x {\displaystyle 1.15x} 1.15x. Since there are 100 − x {\displaystyle 100-x} 100-x cups of soda in the punch, and soda is priced at $0.75 per cup, the total price of the soda in the mixture is 0.75 ( 100 − x ) {\displaystyle 0.75(100-x)} 0.75(100-x). Simplified using the distributive property, this becomes 75 − .75 x {\displaystyle 75-.75x} 75-.75x.

Set up the equation. To solve for x {\displaystyle x} x set up an equation using the third column of the table. The values in the first and second row of the third column will add up to the value in the third row of the third column. For example, ( 1.15 x ) + ( 75 − .75 x ) = 100 {\displaystyle (1.15x)+(75-.75x)=100} (1.15x)+(75-.75x)=100.
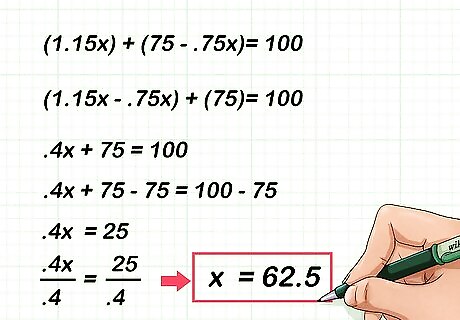
Solve the equation. To do this, isolate the variable using normal algebra rules. Remember to balance the equation by completing calculations to both sides. For example, to solve for x {\displaystyle x} x, you would first combine like x {\displaystyle x} x terms, then subtract 75 from both sides of the equation, then divide both sides .4: ( 1.15 x ) + ( 75 − .75 x ) = 100 {\displaystyle (1.15x)+(75-.75x)=100} (1.15x)+(75-.75x)=100 ( 1.15 x − .75 x ) + ( 75 ) = 100 {\displaystyle (1.15x-.75x)+(75)=100} (1.15x-.75x)+(75)=100 .4 x + 75 = 100 {\displaystyle .4x+75=100} .4x+75=100 .4 x + 75 − 75 = 100 − 75 {\displaystyle .4x+75-75=100-75} .4x+75-75=100-75 .4 x = 25 {\displaystyle .4x=25} .4x=25 .4 x .4 = 25 .4 {\displaystyle {\frac {.4x}{.4}}={\frac {25}{.4}}} {\frac {.4x}{.4}}={\frac {25}{.4}} x = 62.5 {\displaystyle x=62.5} x=62.5
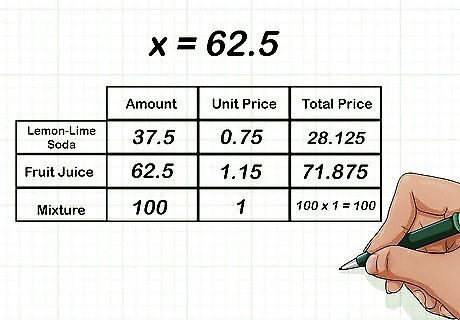
Find the missing amounts of each ingredient. To do this, plug the value of x {\displaystyle x} x into the table, and complete any necessary calculations. For example, since x = 62.5 {\displaystyle x=62.5} x=62.5, the student council should use 62.5 cups of fruit juice in its punch, and 100 − 62.5 {\displaystyle 100-62.5} 100-62.5, or 37.5, cups of lemon-lime soda in the punch.



















Comments
0 comment