How to Calculate and Measure Water Pump Horsepower

• Water horsepower = ${\displaystyle {\frac {TDH*Q*SG}{3960}}}$
• TDH = Total Dynamic Head = Vertical distance liquid travels (in feet) + friction loss from pipe
• Q = flow rate of liquid in gallons per minute
• SG = specific gravity of liquid (this equals 1 if you are pumping water)

Calculating Water Horsepower for a Planned Project

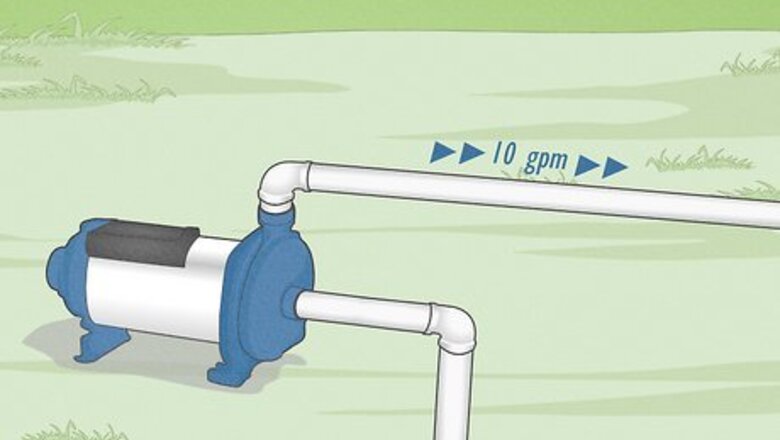
Decide on the desired flow rate. The needs of your project determine the necessary flow rate of liquid from the pump. Write this value down in gallons per minute (gpm). You won't be using this value right away, but it will determine which pumps and pipes you consider. In other words, you need to know how much water you need to move per minute, which will vary by project. Refer to this gpm chart for common flow rate estimates. Example: A gardener has an irrigation plan that requires a flow rate of 10 gallons per minute.

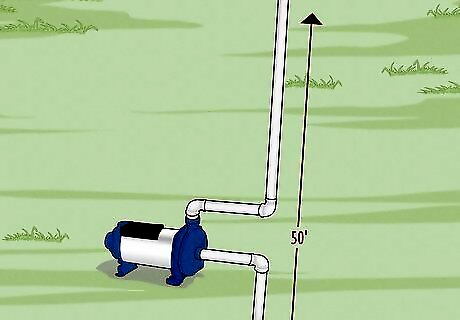
Measure the height the water needs to travel. This is the vertical distance from the top of the water table (or the top of the water level in the first tank) to the final destination of the water. Ignore any horizontal distance. If the water level changes over time, use the maximum expected distance. This is the "pumping lift" your pump will need to generate. Example: When the gardener's water tank is nearly empty (the lowest expected level), its water level is 50 feet below the area of the garden that needs watering.

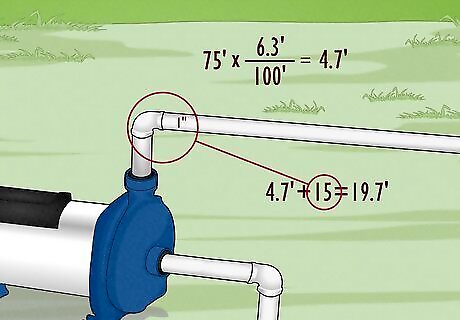
Estimate friction losses from the pipe. Besides the minimum pressure needed to move water a certain distance, your pump also needs to overcome the force of friction as the water moves through the pipe. The amount of friction depends on the pipe's material, internal diameter, and length, as well as the type of bends and fittings you use. Look up these values on a pipe friction loss chart such as this one. Multiply the total length of your pipe by the friction loss figure to find the total friction loss per feet of head (meaning the number of feet you "lose" from your pumping lift because of friction). These charts often include an estimate of water velocity as well, based on flow rate and the pipes you use. It's best to keep velocity below 5 ft / s to prevent "water hammer," the repeated knocking vibration that can damage your equipment. Example: The gardener decides to use 1" diameter plastic pipes, and needs 75 ft of pipe total (including horizontal lengths). A pipe friction loss chart tells him that 1" plastic pipes cause a loss of 6.3 ft of head for every 100 ft of pipe length. 75 f t ∗ 6.3 f t h e a d 100 f t = 4.7 f t h e a d {\displaystyle 75ft*{\frac {6.3ft_{head}}{100ft}}=4.7ft_{head}} 75ft*{\frac {6.3ft_{{head}}}{100ft}}=4.7ft_{{head}}He also looks up the friction loss from each fitting in the pipe. For 1" plastic, one 90º elbow connector and three threaded fittings contribute a total loss of 15 ft.Adding this all together, the total friction loss is 4.7 + 15 = 19.7 ft., or about 20 ft.

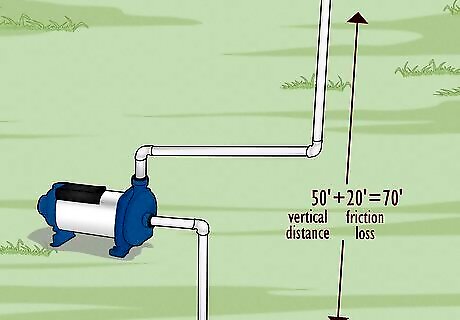
Add the pumping lift and friction loss together. The vertical distance water needs to travel plus the friction losses from the pipe make the "total dynamic head" or TDH. This is the total pressure load the pump needs to overcome. Example: TDH = vertical distance + friction loss = 50 ft + 20 ft = 70 ft.

Look up the specific gravity if you are pumping anything besides water. The basic water horsepower formula assumes you are pumping water. If you are pumping a different fluid, look up its "specific gravity" online or in an engineering reference table. Fluids with a higher specific density are denser, and require more horsepower to push through the pipe. Example: Since the gardener is pumping water, he doesn't need to look anything up. Water's specific gravity is equal to 1.

Enter these values into the water horsepower formula. The water horsepower, or minimum power required to run the pump, equals T D H ∗ Q ∗ S G 3960 {\displaystyle {\frac {TDH*Q*SG}{3960}}} {\frac {TDH*Q*SG}{3960}}, where TDH is the total dynamic head in feet, Q is the flow rate in gpm, and SG is the specific gravity (1 for water). Enter all the values you found into this formula to find the water horsepower for your project. Example: The garden pump needs to overcome a TDH of 70 ft and produce a flow rate Q of 10 gpm. Since it is pumping water, the SG is equal to 1.Water horsepower = T D H ∗ Q ∗ S G 3960 = 70 ∗ 10 ∗ 1 3960 = {\displaystyle {\frac {TDH*Q*SG}{3960}}={\frac {70*10*1}{3960}}=} {\frac {TDH*Q*SG}{3960}}={\frac {70*10*1}{3960}}= ~0.18 horsepower.

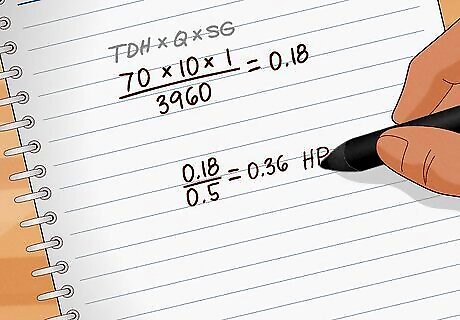
Divide horsepower by pump efficiency. Now you know how much horsepower you need to supply to run your pump. However, no mechanical device is 100% efficient at transferring power. Once you have chosen a pump, check the manufacturer's info for the pump's efficiency and write it as a decimal. Divide the water horsepower by this value to find the actual horsepower of the motor you need for your pump. Most modern pumps are between 50% and 85% efficient when used as intended. If you cannot find an efficiency rating for your pump, you can assume the actual motor horsepower needed falls between W a t e r H P 0.5 {\displaystyle {\frac {WaterHP}{0.5}}} {\frac {WaterHP}{0.5}} and W a t e r H P 0.85 {\displaystyle {\frac {WaterHP}{0.85}}} {\frac {WaterHP}{0.85}} Example: To do 0.18 horsepower of work, a pump with a 50% (or 0.5) efficiency rating would actually require 0.18 0.5 = {\displaystyle {\frac {0.18}{0.5}}=} {\frac {0.18}{0.5}}= a 0.36 hp motor.

Measuring a Pump's Water Horsepower

Check the water level in the base reservoir tank. This is the tank that supplies water for your pump. The water level in the tank will also equal the water level in the pipe, so this is the level the pump is currently drawing from. Read the indicator on your reservoir to find this. If you are pumping from a well, either measure the depth directly or look for an estimate of water table levels in your area (at this time of year). Government agencies such as the USGS can often provide this information.

Empty the destination reservoir. The destination reservoir is a second tank, to which the pump transfers water from the base reservoir. Make sure it is empty and connected properly to the pump. If you do not normally have a tank here, just put down a large bucket to collect the water for this measurement. Use a bucket of known size in gallons.

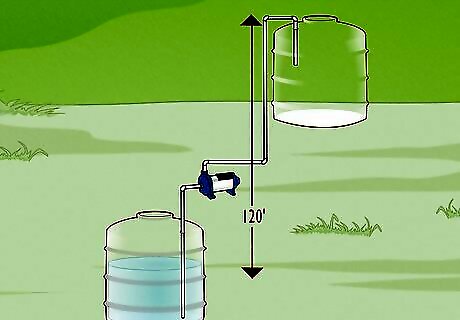
Measure the vertical distance between the two locations. Using a scale or ruler, measure the vertical distance between the water level in the base reservoir tank and the water input at the destination tank. Write down the distance in feet. For example, say the water level in the first tank is 120 feet lower in elevation than the destination reservoir. For this step, it doesn't matter how much horizontal distance the water travels.

Time how fast it takes to fill the second reservoir. Switch on the pump to start pumping water. Start a stopwatch at the same time. Observe how long it takes for the second reservoir to fill, and jot down this number, as well as the capacity of the second reservoir.

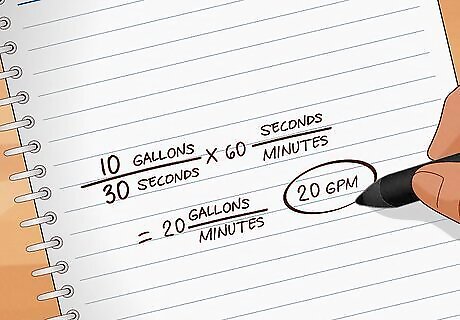
Measure the flow rate. Once your pump is working, measure the volumetric flow rate: the volume of water transported per unit of time. Note this rate in gallons per minute. For example, your pump takes 30 seconds to fill a 10-gallon container. This means the flow rate is 10 g a l l o n s 30 s e c o n d s ∗ 60 s e c o n d s m i n u t e = 20 g a l l o n s m i n u t e {\displaystyle {\frac {10\ gallons}{30\ seconds}}*60{\frac {seconds}{minute}}=20{\frac {gallons}{minute}}} {\frac {10\ gallons}{30\ seconds}}*60{\frac {seconds}{minute}}=20{\frac {gallons}{minute}}. This is usually written 20 gpm, for "gallons per minute".

Look up the specific gravity of the fluid. Specific gravity is a measurement of density: the more dense a fluid is, the more power it takes to pump. Water has a specific gravity of 1. If pumping a different fluid, look it up on a specific gravity engineering table. This example will use water, so the specific gravity is 1.

Estimate horsepower from these values. The water horsepower of the pump is roughly equal to H ∗ Q ∗ S G 3960 {\displaystyle {\frac {H*Q*SG}{3960}}} {\frac {H*Q*SG}{3960}}, where H is the vertical distance the water travels in feet, Q is the flow rate in gallons per minute, and SG is the specific gravity of the fluid. In this example, the pump is operating at 120 f t ∗ 20 g p m ∗ 1 3960 = {\displaystyle {\frac {120ft*20gpm*1}{3960}}=} {\frac {120ft*20gpm*1}{3960}}= 0.65 horsepower. In reality, you are likely using more power than this on your pump. Your pump is also overcoming the force of friction in the pipes, and some power is wasted due to the inefficiency of the motor. You can double this result for a rough estimate of power consumption, or track the actual amount of fuel or electricity your motor uses, or refer to the full calculations above.