How to Calculate Angular Acceleration

Calculating Instantaneous Angular Acceleration

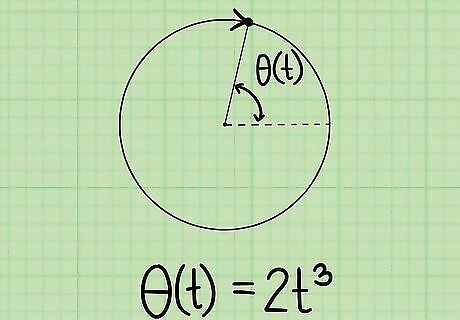
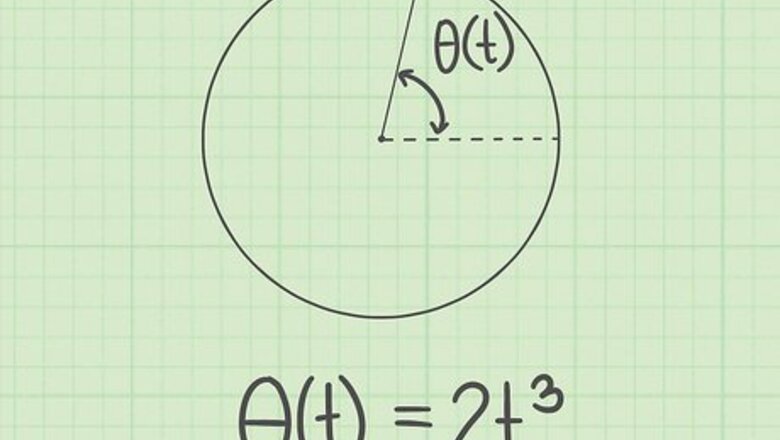
Determine the function for angular position. In some cases, you may be provided with a function or formula that predicts or assigns the position of an object with respect to time. In other cases, you may derive the function from repeated experiments or observations. For this article, we assume that the function has been provided or previously calculated. For the example illustrated above, studies have led to the function θ ( t ) = 2 t 3 {\displaystyle \theta (t)=2t^{3}} \theta (t)=2t^{3}, where θ ( t ) {\displaystyle \theta (t)} \theta (t) is the angular measure of the position of the rotation at a given time, and t {\displaystyle t} t represents the time.

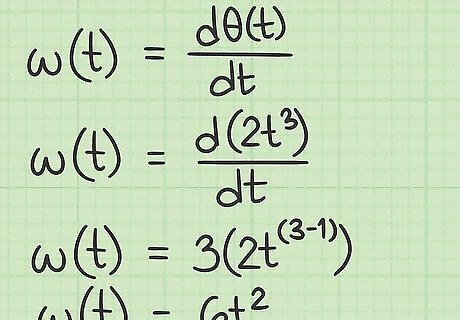
Find the function for angular velocity. Velocity is the measure of how fast an object changes its position. In layman's terms, we think of this as its speed. In mathematical terms, the change of position over time can be found by finding the derivative of the position function. The symbol for angular velocity is ω {\displaystyle \omega } \omega . Angular velocity is generally measured in units of radians divided by time (radians per minute, radians per second, etc.). In this example, find the first derivative of the position function θ ( t ) = 2 t 3 {\displaystyle \theta (t)=2t^{3}} \theta (t)=2t^{3}: ω ( t ) = d θ d t = 6 t 2 {\displaystyle \omega (t)={\frac {d\theta }{dt}}=6t^{2}} \omega (t)={\frac {d\theta }{dt}}=6t^{2} If desired, this function could be used to calculate the angular velocity of the spinning object at any desired time t {\displaystyle t} t. For this particular calculation, the angular velocity function is just an intermediate step toward finding angular acceleration.

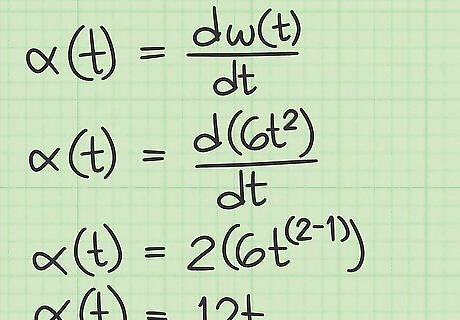
Find the function for angular acceleration. Acceleration is the measure of how fast an object's velocity is changing over time. You can mathematically calculate the angular acceleration by finding the derivative of the function for angular velocity. Angular acceleration is generally symbolized with α {\displaystyle \alpha } \alpha , the Greek letter alpha. Angular acceleration is reported in units of velocity per time, or generally radians divided by time squared (radians per second squared, radians per minute squared, etc.). In the previous step, you used the function for position to find the angular velocity ω ( t ) = 6 t 2 {\displaystyle \omega (t)=6t^{2}} \omega (t)=6t^{2}. Now find the acceleration function as the derivative of ω {\displaystyle \omega } \omega : α = d ω d t = 12 t {\displaystyle \alpha ={\frac {d\omega }{dt}}=12t} \alpha ={\frac {d\omega }{dt}}=12t.

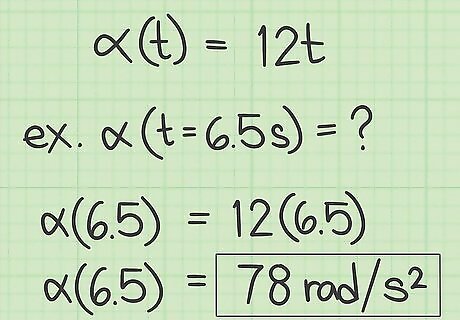
Apply the data to find instantaneous acceleration. Once you have derived the function for instantaneous acceleration as the derivative of velocity, which in turn is the derivative of position, you are ready to calculate the instantaneous angular acceleration of the object at any chosen time. For the sample problem in the illustration, suppose you know that the function for the position of the spinning object is θ ( t ) = 2 t 3 {\displaystyle \theta (t)=2t^{3}} \theta (t)=2t^{3}, and you are asked for the object's angular acceleration after it has been spinning for 6.5 seconds. Use the derived formula for α {\displaystyle \alpha } \alpha and insert the information as follows: α = d ω d t = 12 t {\displaystyle \alpha ={\frac {d\omega }{dt}}=12t} \alpha ={\frac {d\omega }{dt}}=12t α = ( 12 ) ( 6.5 ) {\displaystyle \alpha =(12)(6.5)} \alpha =(12)(6.5) α = 78.0 {\displaystyle \alpha =78.0} \alpha =78.0 Your result should be reported in units of radians per second squared. Thus, the angular acceleration for this spinning object when it has been spinning for 6.5 seconds is 78.0 radians per second squared.

Calculating Average Angular Acceleration

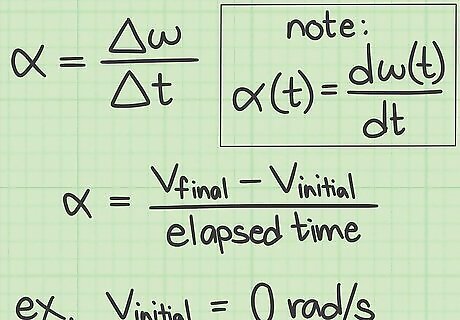
Measure initial angular velocity. The first method for calculating angular acceleration ( α {\displaystyle \alpha } \alpha ) is to divide the change in angular velocity ( ω {\displaystyle \omega } \omega ) over some period of time by the amount of time that is measured. The formula for this can be written as follows: α = Δ ω Δ t = final velocity-initial velocity elapsed time {\displaystyle \alpha ={\frac {\Delta \omega }{\Delta t}}={\frac {\text{final velocity-initial velocity}}{\text{elapsed time}}}} \alpha ={\frac {\Delta \omega }{\Delta t}}={\frac {{\text{final velocity-initial velocity}}}{{\text{elapsed time}}}} Consider a compact disc at the moment you place it in the CD player. Its initial velocity is zero. As an alternative example, suppose you know from test measurements that the wheels of a roller coaster spin at a velocity of 400 revolutions per second, which is equivalent to 2513 radians per second. To measure negative acceleration over a braking distance, you can use this measurement as the initial velocity.

Measure final angular velocity. The second piece of information that you need is the angular velocity of the spinning or rotating object at the end of the time period that you want to measure. This is to be called the “final” velocity. A compact disc plays in the machine by rotating at an angular velocity of 160 radians per second. The roller coaster, after applying its brakes to the spinning wheels, ultimately reaches an angular velocity of zero when it stops. This will be its final angular velocity.

Measure the elapsed time. To calculate the average angular velocity of the spinning or rotating object, you need to know the amount of time that passes during your observation. This can be found by direct observation and measurement, or the information can be provided for a given problem. The owner's manual for the CD player provides the information that the CD reaches its playing speed in 4.0 seconds. From observations of roller coasters being tested, it has been found that they can come to a complete stop within 2.2 seconds from when the brakes are initially applied.

Calculate the average angular acceleration. If you know the initial angular velocity, the final angular velocity, and the elapsed time, fill that data into the equation and find the average angular acceleration. For the example of the CD player, the calculation is as follows: α = Δ ω Δ t = final velocity-initial velocity elapsed time {\displaystyle \alpha ={\frac {\Delta \omega }{\Delta t}}={\frac {\text{final velocity-initial velocity}}{\text{elapsed time}}}} \alpha ={\frac {\Delta \omega }{\Delta t}}={\frac {{\text{final velocity-initial velocity}}}{{\text{elapsed time}}}} α = 160 − 0 4.0 {\displaystyle \alpha ={\frac {160-0}{4.0}}} \alpha ={\frac {160-0}{4.0}} α = 160 4.0 {\displaystyle \alpha ={\frac {160}{4.0}}} \alpha ={\frac {160}{4.0}} α = 40 {\displaystyle \alpha =40} \alpha =40 radians per second squared. For the roller coaster example, the calculation looks like this: α = Δ ω Δ t = final velocity-initial velocity elapsed time {\displaystyle \alpha ={\frac {\Delta \omega }{\Delta t}}={\frac {\text{final velocity-initial velocity}}{\text{elapsed time}}}} \alpha ={\frac {\Delta \omega }{\Delta t}}={\frac {{\text{final velocity-initial velocity}}}{{\text{elapsed time}}}} α = 0 − 2513 2.2 {\displaystyle \alpha ={\frac {0-2513}{2.2}}} \alpha ={\frac {0-2513}{2.2}} α = − 2513 2.2 {\displaystyle \alpha ={\frac {-2513}{2.2}}} \alpha ={\frac {-2513}{2.2}} α = − 1142.3 {\displaystyle \alpha =-1142.3} \alpha =-1142.3 radians per second squared. Note that acceleration is always going to be in units of some distance measurement “per” time squared. With angular acceleration, the distance is generally measured in radians, although you could convert that to number of rotations if you wish.

Reviewing Angular Acceleration

Understand the concept of angular motion. When people think of the speed of an object, they often consider linear motion - that is, objects traveling mostly in a straight line. This would include a car, a plane, a ball that is thrown or any number of other objects. However, angular motion describes objects that spin or rotate. Think of the earth spinning on its axis. The position or speed of the earth can be measured with angular quantities. A spinning compact disc (or record player, if you're old enough), electrons on their axes, or the wheels of a car on the axle are other examples of rotating objects that can be measured through angular motion.

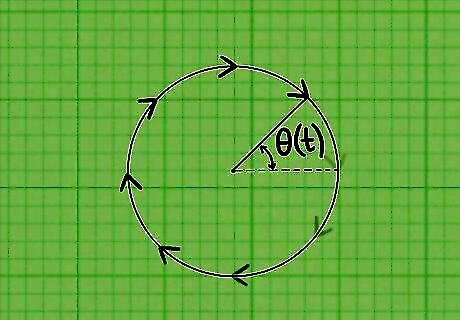
Visualize angular position. When you measure the position of a moving vehicle, for example, you can measure the distance traveled in a straight line from the starting point. With a rotating object, the measurement is generally done in terms of the angle around a circle. By convention, the starting or “zero” point is generally a horizontal radius from the center to the right side of the circle. The distance traveled is measured by the size of the angle θ {\displaystyle \theta } \theta , measured from that horizontal radius. The angle that is being measured is commonly represented by θ {\displaystyle \theta } \theta , the Greek letter theta. Positive motion is measured in a counterclockwise direction. Negative motion is measured in a clockwise direction.

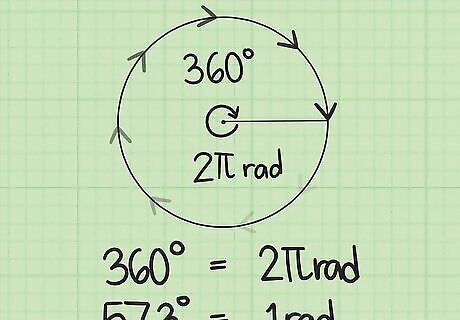
Measure angular motion in radians. Linear travel is generally measured in some unit of distance, such as miles, meters, inches or some other unit of length. Rotational or angular motion is generally measured in units called radian. A radian is a fraction of the circle. For standard reference, mathematicians use the “unit circle,” which has a standard radius of 1 unit. One full rotation around the unit circle is said to measure 2π radians. Therefore, a half circle is π radians, and a quarter circle is π/2 radians. Sometimes it is useful to convert from radians to degrees. If you recall that a full circle is 360 degrees, you can find the conversion as follows: 360 degrees = 2 π radians {\displaystyle 360\ {\text{degrees}}=2\pi \ {\text{radians}}} 360\ {\text{degrees}}=2\pi \ {\text{radians}} 360 2 π degrees = 1 radian {\displaystyle {\frac {360}{2\pi }}\ {\text{degrees}}=1\ {\text{radian}}} {\frac {360}{2\pi }}\ {\text{degrees}}=1\ {\text{radian}} 57.3 degrees = 1 radian {\displaystyle 57.3\ {\text{degrees}}=1\ {\text{radian}}} 57.3\ {\text{degrees}}=1\ {\text{radian}} Thus, one radian is about equal to 57.3 degrees.

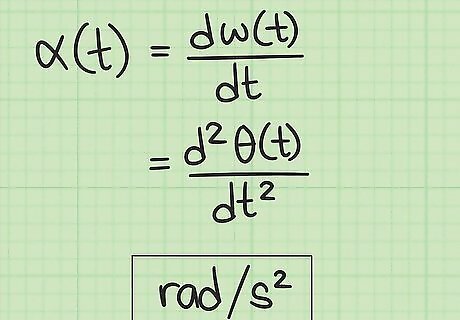
Understand the concept of angular acceleration. Angular acceleration is the measurement of how fast or slow a rotating object is changing its velocity. In other words, is the spinning speeding up or slowing down? If you know the angular velocity at a starting time and then at a later ending time, you can calculate the average angular acceleration over that time interval. If you know the function for the object's position, you can use calculus to derive the instantaneous angular acceleration at any chosen time. People often use the word “acceleration” to mean speeding up, and “deceleration” to mean slowing down. In mathematical and physical terms, however, only the word “acceleration” is used. If the object is speeding up, the acceleration is positive. If it is slowing down, the acceleration is negative.