How to Calculate Mortgage Payments

Calculating Mortgage Payments Using a Spreadsheet Program

Understand the function used. Mortgage payments can be easily found using your chosen spreadsheet program. This function, in all major spreadsheet programs (Microsoft Excel, Google Spreadsheet, and Apple Numbers), is known as PMT, or the payment function. It combines information like your interest rate, number of periods, and principal to arrive at an amount for each monthly payment. For simplicity, we will be focusing on Microsoft Excel's PMT function here. The process and inputs will likely be identical or very similar for any other program you are using. Consult the help tab or customer service if you have any problems using these functions.

Start using the PMT function. Start using the PMT function by typing =PMT( into your spreadsheet. The program will then prompt you for the proper entries into each part of the function by showing the following: PMT(rate, nper, pv, [fv], [type]). The first three represent required inputs, while the last two are optional. rate stands for the monthly interest rate. Note that this will be your annual interest rate (the quoted rate on your loan agreement, like 4 or 5 percent) divided by 12. It should also be expressed as a decimal. For example, if your annual interest rate is 6%, you would divide this number by twelve to get your monthly interest rate. This would be 6%/12, or 0.5%. However, this number must be input in the equation as decimal, so we divide again by 100. So we have 0.5%/100, which equals 0.005. This will be your monthly interest you will use to calculate mortgage payments. These calculations can also be done in a different order (6%/100 = 0.06, 0.03/12 = 0.005). nper is short for "number of periods" and simply represents how many payments you will make on your loan. For a monthly payment, this would be 12 times the number of years on your loan. Imagine for this example that you have a 15-year mortgage. So, your "nper" value, or your number of payments, would be 12*15, or 180. pv stands for "present value" but here it simply means the principal of your loan. For this example, imagine you have a $100,000 loan. This will be your "pv". Don't worry about the other two values; leaving them blank will make the program assume their correct value of 0.

Enter this information and press enter. The program will display your monthly payment amount in the same cell you entered the formula into. Note that this number will be negative, this is simply the program expressing it as a payment (or expense). In the example above, this information would be entered as =PMT(0.005, 180, 100000).

Analyze your result. The PMT function will return an amount that represents the total amount you will pay on the loan each month. Know that this number will be expressed as a negative number. This doesn't mean you entered your information incorrectly, but simply that the program represents payments as an expense and therefore, a negative number. Multiply by -1 if this helps you understand and use the figure. The spreadsheet should return -$843.86 when you enter your function as described above. Multiply this number by -1 to get your monthly payment of $843.86.

Calculating Mortgage Payments with an Equation

Understand the equation. In order to calculate the monthly payment, we can rely on a relatively simple equation. The monthly payment equation can be represented as follows: M = P r ( 1 + r ) n ( 1 + r ) n − 1 {\displaystyle M=P{\frac {r(1+r)^{n}}{(1+r)^{n}-1}}} M=P{\frac {r(1+r)^{{n}}}{(1+r)^{{n}}-1}}. These variables represent the following inputs: M is your monthly payment. P is your principal. r is your monthly interest rate, calculated by dividing your annual interest rate by 12. n is your number of payments (the number of months you will be paying the loan)

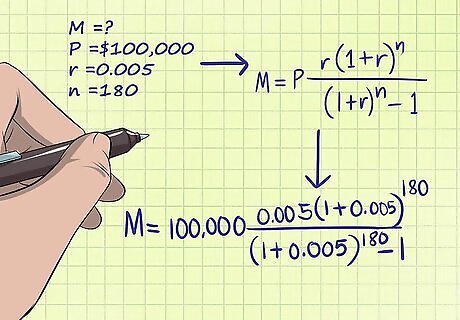
Input your information into the equation. You will need to input your principal, monthly interest rate, and number of payments in order to find your monthly payment. This information can be easily found in your loan agreement or from a quoted loan estimate. Check the information again to be sure of its accuracy before using it in calculations. For example, imagine you have a $100,000 mortgage loan with 6 percent annual interest over 15 years. Your input for "P" would be $100,000. For "r," you would use your monthly interest rate, which would be 0.06 (6 percent) divided by 12, or 0.005 (0.5 percent). For "n" you would use your total number of payments, one for each month in fifteen years, which would be 12*15, or 180. In this example, your complete equation would look like this: M = $ 100 , 000 0.005 ( 1 + 0.005 ) 180 ( 1 + 0.005 ) 180 − 1 {\displaystyle M=\$100,000{\frac {0.005(1+0.005)^{180}}{(1+0.005)^{180}-1}}} M=\$100,000{\frac {0.005(1+0.005)^{{180}}}{(1+0.005)^{{180}}-1}}

Simplify your equation by adding 1 to the "r." Simplify your terms by doing the first step in the order of operations, which is adding the 1 and "r" inside the parentheses on the top and bottom of the equation. This is a simple step that will make your equation look much less complicated. After this step, your sample equation would look like this: M = $ 100 , 000 0.005 ( 1.005 ) 180 ( 1.005 ) 180 − 1 {\displaystyle M=\$100,000{\frac {0.005(1.005)^{180}}{(1.005)^{180}-1}}} M=\$100,000{\frac {0.005(1.005)^{{180}}}{(1.005)^{{180}}-1}}

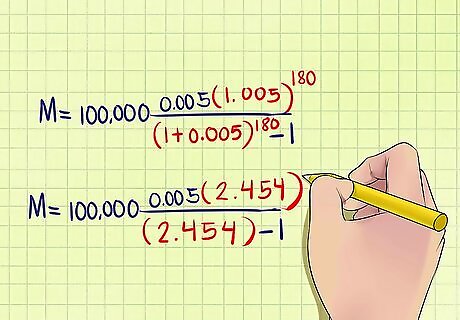
Solve the exponents. The results inside the parentheses, (1+ r), from the previous step must now be raised to the power of "n." Again, this "n" represents the total number of payments. This step requires a calculator with an exponent function, which is usually represented like this: x y {\displaystyle x^{y}} x^{y}. This is done by entering the value to be raised, (1.005) in the example equation, then pressing the exponent button, then entering your value for "n" and pressing enter or =. In the example, the result comes out as 2.454. If you don't have such a calculator, type your values from the last equation into Google followed by ^(n) while replacing the "n" in parentheses with your value for "n." The search engine will calculate this value for you. Keep in mind that only the figures inside the parentheses will be raised to this power, not the "r" outside of them (at the front) or the -1 at the end of the equation. After this step the sample equation would look like this: M = $ 100 , 000 0.005 ( 2.454 ) 2.454 − 1 {\displaystyle M=\$100,000{\frac {0.005(2.454)}{2.454-1}}} M=\$100,000{\frac {0.005(2.454)}{2.454-1}}

Simplify again. Here, you should multiple "r" times the result of the last step on the top (the numerator) and subtract 1 from your result on the bottom (the denominator). The same equation would look like this after this step: M = $ 100 , 000 0.01227 1.454 {\displaystyle M=\$100,000{\frac {0.01227}{1.454}}} M=\$100,000{\frac {0.01227}{1.454}}

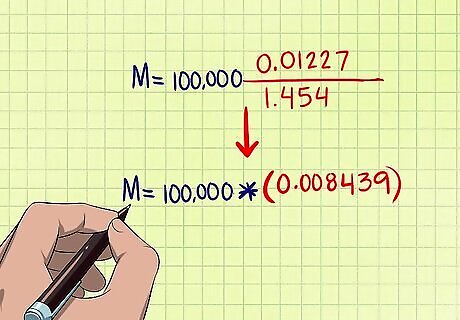
Divide the numerator by the denominator. This means dividing the top part of the equation by the bottom part of the equation. This should leave you with a small decimal. In the example, your equation would now be: M = $ 100 , 000 ∗ ( 0.008439 ) {\displaystyle M=\$100,000*(0.008439)} M=\$100,000*(0.008439)

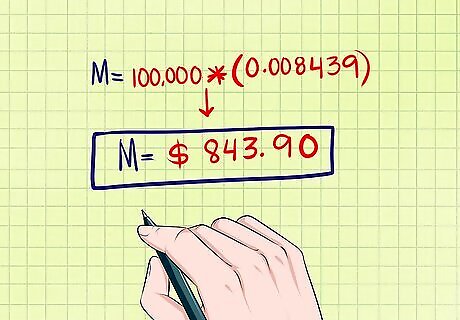
Multiply "P" by this result. This will give you your monthly loan payment. In the example, this would be ($100,000)*(0.008439), or $843.90. This represents your monthly payment. Financial literacy is empowering. "This was really useful to me. Not only was I looking to calculate whether I could afford a mortgage on my dream property, but I also learned about how I could use these tutorials for math and ICT lessons, so thank you!" - Marie W. I needed to learn this calculation for work. "My boss asked me if I knew how to calculate a mortgage. I said I could look it up and found this article. I made a spreadsheet calculating a mortgage payment using both the formula and function methods I learned here. My boss was really impressed with my work!" - Daniel G. Did you know that wikiHow has collected over 365,000 reader stories since it started in 2005? We’d love to hear from you! Share your story here.

Creating an Amortization Schedule

Set up your amortization schedule. An amortization schedule will tell you exactly how your monthly mortgage payments will be split between paying off principal and interest and what your balance will be at the end of each month. Start by inputting the basics of your loan information in the top left of a spreadsheet program. For example, in cell A1, write out "annual interest rate." Then, input your annual interest rate as a percentage in the next cell over, B1. Continue down to cell A2 for the loan duration in years, inputting the amount in column B as before. Do the same for payment per year and loan principal in cells A3 and A4, respectively.

Create your amortization schedule columns. Skip a line under your loan information. Then, place the following words across the spreadsheet, in row 6 from columns A to E: Payment number. Payment amount. Principal payment. Interest payment. Loan balance.

Fill out your first month's amortization. Directly under the column headers you just created, start filling out your loan information. Under payment number, place a 1. Then, under payment amount, type in "=pmt(B1/B3,B2*B3,B4)". This is the payment function. Under principal payment, type "=ppmt(B1/B3,A7,B2*B3,B4)". This is the principal payment function and it shows the amount of the principal paid down each month. Under interest payment, type "=ipmt(B1/B3,A7,B2*B3,B4)". This is the interest payment function and it shows the amount of interest paid down each month. Finally, under loan balance, type "=(B4+C7)". Cell A7 should contain your first payment number, 1. Cell C7 should contain the payment amount.

Complete your amortization schedule. Select the range from cell A7 to E7. Then, drag the calculations down to the last payment. At this point, the loan balance in column E should be $0. Remember that your number of payments is calculated by multiplying the number of annual payments by the loan duration in years. If your loan payment numbers don't update down the amortization schedule. Type "=(A7+1)" into cell A8 (payment 2) and drag that down to the end of your schedule. The rest of the numbers will then update.