How to Calculate Percent Yield in Chemistry

Finding the Limiting Reactant

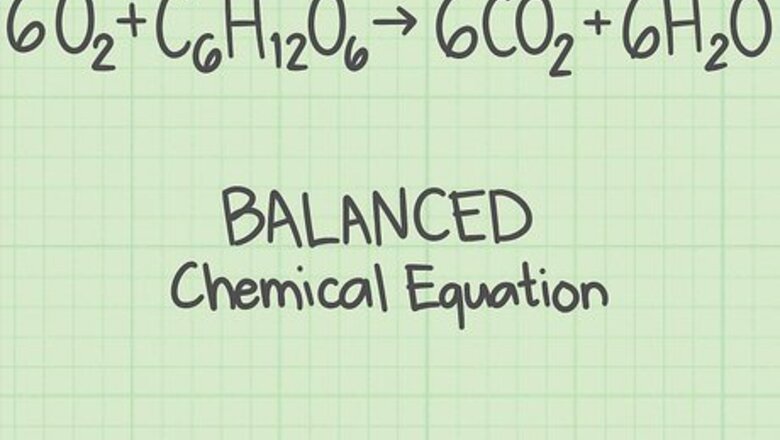
Start with a balanced chemical equation. A chemical equation describes the reactants (on the left side) reacting to form products (on the right side). Some problems will give you this equation, while others ask you to write it out yourself, such as for a word problem. Since atoms are not created or destroyed during a chemical reaction, each element should have the same number of atoms on the left and right side. For example, oxygen and glucose can react to form carbon dioxide and water: 6 O 2 + C 6 H 12 O 6 {\displaystyle 6O_{2}+C_{6}H_{12}O_{6}} 6O_{2}+C_{6}H_{{12}}O_{6} → 6 C O 2 + 6 H 2 O {\displaystyle 6CO_{2}+6H_{2}O} 6CO_{2}+6H_{2}O Each side has exactly 6 carbon (C) atoms, 12 hydrogen (H) atoms, and 18 oxygen (O) atoms. The equation is balanced. Read this guide if you are asked to balance an equation yourself.

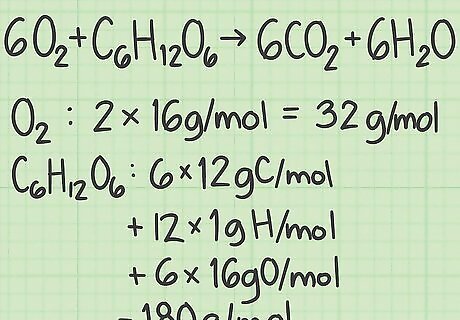
Calculate the molar mass of each reactant. Look up the molar mass of each atom in the compound, then add them together to find the molar mass of that compound. Do this for a single molecule of the compound. For example, 1 molecule of oxygen ( O 2 {\displaystyle O_{2}} O_{2}) contains 2 oxygen atoms. Oxygen's molar mass is about 16 g/mol. (You can find a more precise value on a periodic table.) 2 oxygen atoms x 16 g/mol per atom = 32 g/mol of O 2 {\displaystyle O_{2}} O_{2}. The other reactant, glucose ( C 6 H 12 O 6 {\displaystyle C_{6}H_{12}O_{6}} C_{6}H_{{12}}O_{6}) has a molar mass of (6 atoms C x 12 g C/mol) + (12 atoms H x 1 g H/mol) + (6 atoms O x 16 g O/mol) = 180 g/mol.

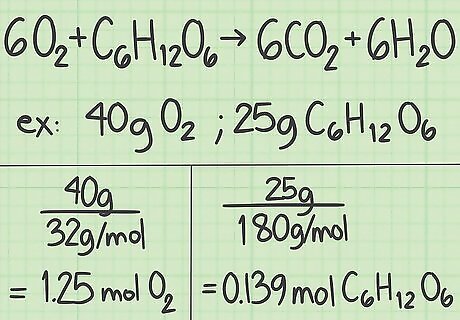
Convert the amount of each reactant from grams to moles. Now it's time to look at the specific experiment you are studying. Write down the amounts of each reactant in grams. Divide this value by that compound's molar mass to convert the amount to moles. For example, say you started with 40 grams of oxygen and 25 grams of glucose. 40 g O 2 {\displaystyle O_{2}} O_{2} / (32 g/mol) = 1.25 moles of oxygen. 25g C 6 H 12 O 6 {\displaystyle C_{6}H_{12}O_{6}} C_{6}H_{{12}}O_{6} / (180 g/mol) = about 0.139 moles of glucose.

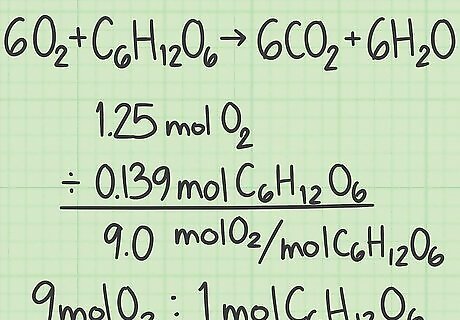
Find the ratio of your reactions. A mole is an exact number for the amount of a substance and it is equal to 6.022 times 10 to the 23rd power elementary entities, which could be atoms, ions, electrons, or molecules. You now know how many molecules of each reactant you started with. Divide the moles of 1 reactant with the moles of the other to find the ratio of the 2 molecules. You started with 1.25 moles of oxygen and 0.139 moles of glucose. The ratio of oxygen to glucose molecules is 1.25 / 0.139 = 9.0. This means you started with 9 molecules of oxygen for every 1 molecule of glucose.

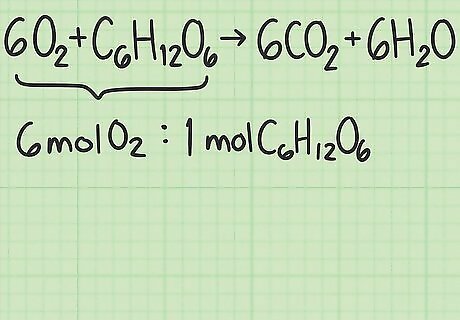
Find the ideal ratio for the reaction. Go back to the balanced equation you wrote down earlier. This balanced equation tells you the ideal ratio of molecules: if you use this ratio, both reactants will be used up at the same time. The left side of the equation is 6 O 2 + C 6 H 12 O 6 {\displaystyle 6O_{2}+C_{6}H_{12}O_{6}} 6O_{2}+C_{6}H_{{12}}O_{6}. The coefficients tell you there are 6 oxygen molecules and 1 glucose molecule. The ideal ratio for this reaction is 6 oxygen / 1 glucose = 6.0. Make sure you list the reactants in the same order you did for the other ratio. If you use oxygen/glucose for 1 and glucose/oxygen for the other, your next result will be wrong.

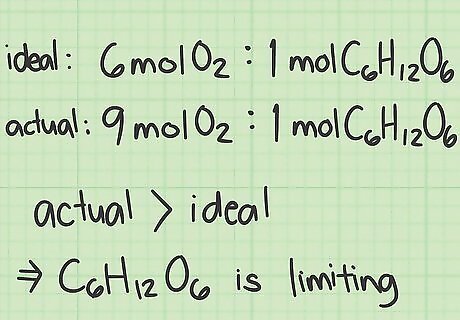
Compare the ratios to find the limiting reactant. In a chemical reaction, 1 of the reactants gets used up before the others. The quantity of the product that is created in the reaction is limited by the reagent. Compare the 2 ratios you calculated to identify the limiting reactant: If the actual ratio is greater than the ideal ratio, then you have more of the top reactant than you need. The bottom reactant in the ratio is the limiting reactant. If the actual ratio is smaller than the ideal ratio, you don't have enough of the top reactant, so it is the limiting reactant. In the example above, the actual ratio of oxygen/glucose (9.0) is greater than the ideal ratio (6.0). The bottom reactant, glucose, must be the limiting reactant.

Calculating Theoretical Yield

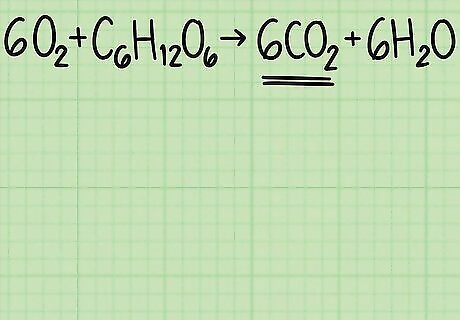
Identify your desired product. The right side of a chemical equation lists the products created by the reaction. Each product has a theoretical yield, meaning the amount of product you would expect to get if the reaction is perfectly efficient. Continuing the example above, you are analyzing the reaction 6 O 2 + C 6 H 12 O 6 {\displaystyle 6O_{2}+C_{6}H_{12}O_{6}} 6O_{2}+C_{6}H_{{12}}O_{6} → 6 C O 2 + 6 H 2 O {\displaystyle 6CO_{2}+6H_{2}O} 6CO_{2}+6H_{2}O. The right-hand side lists 2 products, carbon dioxide and water. Let's calculate the yield of carbon dioxide, C O 2 {\displaystyle CO_{2}} CO_{2}.

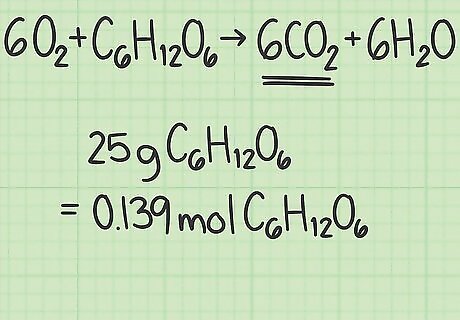
Write down the number of moles of your limiting reactant. The theoretical yield of an experiment is the amount of product created in perfect conditions. To calculate this value, begin with the amount of limiting reactant in moles. (This process is described above in the instructions for finding the limiting reactant.) In the example above, you discovered that glucose was the limiting reactant. You also calculated that you started with 0.139 moles of glucose.

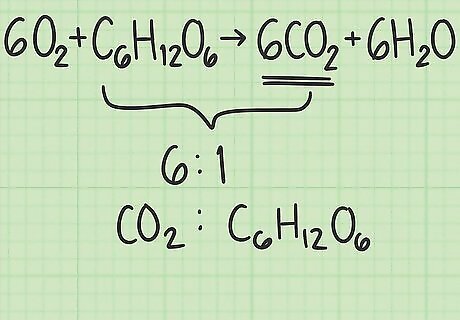
Find the ratio of molecules in your product and reactant. Return to the balanced equation. Divide the number of molecules of your desired product by the number of molecules of your limiting reactant. Your balanced equation is 6 O 2 + C 6 H 12 O 6 {\displaystyle 6O_{2}+C_{6}H_{12}O_{6}} 6O_{2}+C_{6}H_{{12}}O_{6} → 6 C O 2 + 6 H 2 O {\displaystyle 6CO_{2}+6H_{2}O} 6CO_{2}+6H_{2}O. There are 6 molecules of your desired product, carbon dioxide ( C O 2 {\displaystyle CO_{2}} CO_{2}). There is 1 molecule of your limiting reactant, glucose ( C 6 H 12 O 6 {\displaystyle C_{6}H_{12}O_{6}} C_{6}H_{{12}}O_{6}). The ratio of carbon dioxide to glucose is 6/1 = 6. In other words, this reaction can produce 6 molecules of carbon dioxide from 1 molecule of glucose.

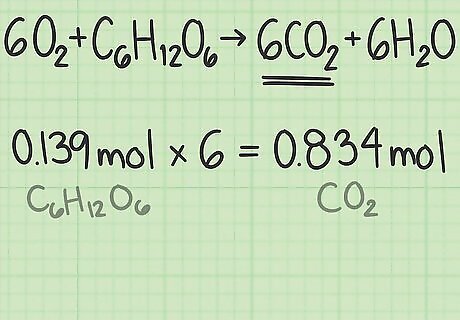
Multiply the ratio by the reactant's quantity in moles. The answer is the theoretical yield of the desired product in moles. You started with 0.139 moles of glucose and the ratio of carbon dioxide to glucose is 6. The theoretical yield of carbon dioxide is (0.139 moles glucose) x (6 moles carbon dioxide / mole glucose) = 0.834 moles carbon dioxide.

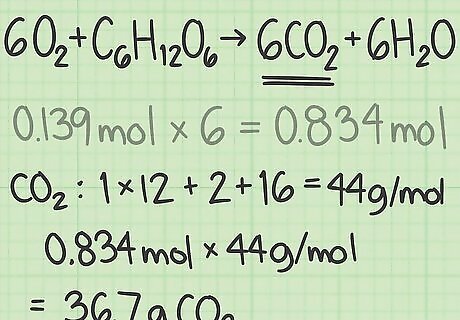
Convert the result to grams. Multiply your answer in moles by the molar mass of that compound to find the theoretical yield in grams. This is a more convenient unit to use in most experiments. For example, the molar mass of CO2 is about 44 g/mol. (Carbon's molar mass is ~12 g/mol and oxygen's is ~16 g/mol, so the total is 12 + 16 + 16 = 44.) Multiply 0.834 moles CO2 x 44 g/mol CO2 = ~36.7 grams. The theoretical yield of the experiment is 36.7 grams of CO2.

Calculating Percent Yield

Understand percent yield. The theoretical yield you calculated assumes that everything went perfectly. In an actual experiment, this never happens: contaminants and other unpredictable problems mean that some of your reactants will fail to convert to the product. This is why chemists use 3 different concepts to refer to yield: The theoretical yield is the maximum amount of product the experiment could make. The actual yield is the actual amount you created, measured directly on a scale. The percent yield = A c t u a l Y i e l d T h e o r e t i c a l Y i e l d ∗ 100 % {\displaystyle {\frac {ActualYield}{TheoreticalYield}}*100\%} {\frac {ActualYield}{TheoreticalYield}}*100\%. A percent yield of 50%, for instance, means you ended up with 50% of the theoretical maximum.

Write down the actual yield of the experiment. If you performed the experiment yourself, gather the purified product from your reaction and weigh it on a balance to calculate its mass. If you are working on a homework problem or someone else's notes, the actual yield should be listed. Let’s say our actual reaction yields 29 grams of CO2.

Divide the actual yield by the theoretical yield. Make sure you use the same units for both values (typically grams). Your answer will be a unit-less ratio. The actual yield was 29 grams, while the theoretical yield was 36.7 grams. 29 g 36.7 g = 0.79 {\displaystyle {\frac {29g}{36.7g}}=0.79} {\frac {29g}{36.7g}}=0.79.

Multiply by 100 to convert to a percentage. The answer is the percent yield. 0.79 x 100 = 79, so the percent yield of the experiment is 79%. You created 79% of the maximum possible amount of CO2.