How to Solve the Heat Equation Using Fourier Transforms

Transform the equation into Fourier space. In this section, we outline the steps to finding the fundamental solution, a term whose name we will shortly come to understand. Taking the Fourier transform of a derivative of order n {\displaystyle n} n is the same as multiplication by ( i ξ ) n . {\displaystyle (i\xi )^{n}.} (i\xi )^{{n}}. Because the Fourier integral is independent of t , {\displaystyle t,} t, we can pull the derivative out of the integral and write ∂ u ∂ t = ∂ u ^ ∂ t . {\displaystyle {\frac {\partial u}{\partial t}}={\frac {\partial {\hat {u}}}{\partial t}}.} {\frac {\partial u}{\partial t}}={\frac {\partial {\hat {u}}}{\partial t}}. ∂ u ^ ∂ t + α ξ 2 u ^ = 0 {\displaystyle {\frac {\partial {\hat {u}}}{\partial t}}+\alpha \xi ^{2}{\hat {u}}=0} {\frac {\partial {\hat {u}}}{\partial t}}+\alpha \xi ^{{2}}{\hat {u}}=0

Solve the resulting ordinary differential equation. Solutions are decaying exponentials in t . {\displaystyle t.} t. The constant term is the initial conditions in Fourier space, denoted by u ^ ( ξ , 0 ) = u ^ 0 ( ξ ) . {\displaystyle {\hat {u}}(\xi ,0)={\hat {u}}_{0}(\xi ).} {\hat {u}}(\xi ,0)={\hat {u}}_{{0}}(\xi ). u ^ ( ξ , t ) = u ^ 0 ( ξ ) e − α ξ 2 t {\displaystyle {\hat {u}}(\xi ,t)={\hat {u}}_{0}(\xi )e^{-\alpha \xi ^{2}t}} {\hat {u}}(\xi ,t)={\hat {u}}_{{0}}(\xi )e^{{-\alpha \xi ^{{2}}t}}

Transform back into real space. The property of the Fourier transform we take advantage of here is convolution: multiplication in Fourier space corresponds to convolution in real space. u ( x , t ) = u 0 ( x ) ∗ U ( x , t ) {\displaystyle u(x,t)=u_{0}(x)*U(x,t)} u(x,t)=u_{{0}}(x)*U(x,t) The term U ( x , t ) = F − 1 { e − α ξ 2 t } {\displaystyle U(x,t)={\mathcal {F}}^{-1}\left\{e^{-\alpha \xi ^{2}t}\right\}} U(x,t)={\mathcal {F}}^{{-1}}\left\{e^{{-\alpha \xi ^{{2}}t}}\right\} is the fundamental solution sought after, also known as the heat kernel. It is the solution to the heat equation given initial conditions of a point source, the Dirac delta function, for the delta function is the identity operator of convolution. δ ( x ) ∗ U ( x , t ) = U ( x , t ) {\displaystyle \delta (x)*U(x,t)=U(x,t)} \delta (x)*U(x,t)=U(x,t)

Evaluate the inverse Fourier integral. The inverse Fourier transform here is simply the integral of a Gaussian. We evaluate it by completing the square. If one looks up the Fourier transform of a Gaussian in a table, then one may use the dilation property to evaluate instead. U ( x , t ) = F − 1 { e − α ξ 2 t } = 1 2 π ∫ − ∞ ∞ e − α ξ 2 t e i x ξ d ξ = 1 2 π ∫ − ∞ ∞ e − α t ( ξ 2 − 2 i x ξ 2 α t − x 2 4 α 2 t 2 ) e − x 2 / 4 α t d ξ = 1 2 π e − x 2 / 4 α t ∫ − ∞ ∞ e − α t ( ξ − i x 2 α t ) 2 d ξ = 1 4 π α t e − x 2 / 4 α t {\displaystyle {\begin{aligned}U(x,t)&={\mathcal {F}}^{-1}\left\{e^{-\alpha \xi ^{2}t}\right\}={\frac {1}{2\pi }}\int _{-\infty }^{\infty }e^{-\alpha \xi ^{2}t}e^{ix\xi }\mathrm {d} \xi \\&={\frac {1}{2\pi }}\int _{-\infty }^{\infty }e^{-\alpha t\left(\xi ^{2}-2{\frac {ix\xi }{2\alpha t}}-{\frac {x^{2}}{4\alpha ^{2}t^{2}}}\right)}e^{-x^{2}/4\alpha t}\mathrm {d} \xi \\&={\frac {1}{2\pi }}e^{-x^{2}/4\alpha t}\int _{-\infty }^{\infty }e^{-\alpha t\left(\xi -{\frac {ix}{2\alpha t}}\right)^{2}}\mathrm {d} \xi \\&={\frac {1}{\sqrt {4\pi \alpha t}}}e^{-x^{2}/4\alpha t}\end{aligned}}} {\begin{aligned}U(x,t)&={\mathcal {F}}^{{-1}}\left\{e^{{-\alpha \xi ^{{2}}t}}\right\}={\frac {1}{2\pi }}\int _{{-\infty }}^{{\infty }}e^{{-\alpha \xi ^{{2}}t}}e^{{ix\xi }}{\mathrm {d}}\xi \\&={\frac {1}{2\pi }}\int _{{-\infty }}^{{\infty }}e^{{-\alpha t\left(\xi ^{{2}}-2{\frac {ix\xi }{2\alpha t}}-{\frac {x^{{2}}}{4\alpha ^{{2}}t^{{2}}}}\right)}}e^{{-x^{{2}}/4\alpha t}}{\mathrm {d}}\xi \\&={\frac {1}{2\pi }}e^{{-x^{{2}}/4\alpha t}}\int _{{-\infty }}^{{\infty }}e^{{-\alpha t\left(\xi -{\frac {ix}{2\alpha t}}\right)^{{2}}}}{\mathrm {d}}\xi \\&={\frac {1}{{\sqrt {4\pi \alpha t}}}}e^{{-x^{{2}}/4\alpha t}}\end{aligned}} This is the well-known fundamental solution to the heat equation. From here, we need only substitute initial conditions and evaluate the resulting convolution integral to obtain a solution. u ( x , t ) = 1 4 π α t ∫ − ∞ ∞ u 0 ( y ) e − ( x − y ) 2 / 4 α t d y {\displaystyle u(x,t)={\frac {1}{\sqrt {4\pi \alpha t}}}\int _{-\infty }^{\infty }u_{0}(y)e^{-(x-y)^{2}/4\alpha t}\mathrm {d} y} u(x,t)={\frac {1}{{\sqrt {4\pi \alpha t}}}}\int _{{-\infty }}^{{\infty }}u_{{0}}(y)e^{{-(x-y)^{{2}}/4\alpha t}}{\mathrm {d}}y

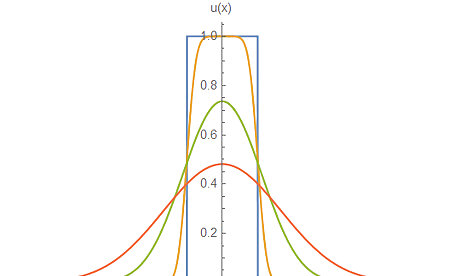
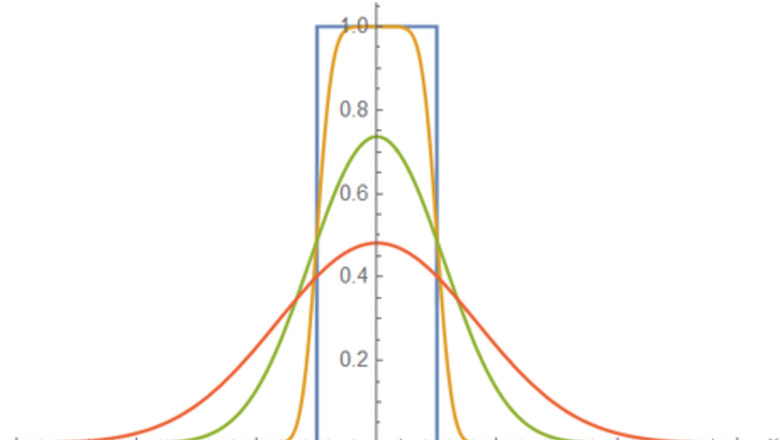
Find u ( x , t ) {\displaystyle u(x,t)} u(x,t) given initial conditions of the rectangular function. The function u 0 ( x ) {\displaystyle u_{0}(x)} u_{{0}}(x) written below is known by other names, including the gate function, or the unit pulse. u 0 ( x ) = { 1 | x | ≤ 1 / 2 0 | x | > 1 / 2 {\displaystyle u_{0}(x)={\begin{cases}1&|x|\leq 1/2\\0&|x|>1/2\end{cases}}} u_{{0}}(x)={\begin{cases}1&|x|\leq 1/2\\0&|x|>1/2\end{cases}} Now, we simply substitute this function into the convolution integral. Here, the form is particularly simple. u ( x , t ) = ∫ − ∞ ∞ u 0 ( y ) U ( x − y , t ) d y = 1 4 π α t ∫ − 1 / 2 1 / 2 e − ( x − y ) 2 / 4 α t d y = 1 π ∫ z − z + e − z 2 d z , z ± = ± 1 / 2 − x 4 α t = 1 2 [ erf ⁡ ( 1 / 2 − x 4 α t ) − erf ⁡ ( − 1 / 2 − x 4 α t ) ] {\displaystyle {\begin{aligned}u(x,t)&=\int _{-\infty }^{\infty }u_{0}(y)U(x-y,t)\mathrm {d} y\\&={\frac {1}{\sqrt {4\pi \alpha t}}}\int _{-1/2}^{1/2}e^{-(x-y)^{2}/4\alpha t}\mathrm {d} y\\&={\frac {1}{\sqrt {\pi }}}\int _{z_{-}}^{z_{+}}e^{-z^{2}}\mathrm {d} z,\quad z_{\pm }={\frac {\pm 1/2-x}{\sqrt {4\alpha t}}}\\&={\frac {1}{2}}\left[\operatorname {erf} \left({\frac {1/2-x}{\sqrt {4\alpha t}}}\right)-\operatorname {erf} \left({\frac {-1/2-x}{\sqrt {4\alpha t}}}\right)\right]\end{aligned}}} {\begin{aligned}u(x,t)&=\int _{{-\infty }}^{{\infty }}u_{{0}}(y)U(x-y,t){\mathrm {d}}y\\&={\frac {1}{{\sqrt {4\pi \alpha t}}}}\int _{{-1/2}}^{{1/2}}e^{{-(x-y)^{{2}}/4\alpha t}}{\mathrm {d}}y\\&={\frac {1}{{\sqrt {\pi }}}}\int _{{z_{{-}}}}^{{z_{{+}}}}e^{{-z^{{2}}}}{\mathrm {d}}z,\quad z_{{\pm }}={\frac {\pm 1/2-x}{{\sqrt {4\alpha t}}}}\\&={\frac {1}{2}}\left[\operatorname {erf}\left({\frac {1/2-x}{{\sqrt {4\alpha t}}}}\right)-\operatorname {erf}\left({\frac {-1/2-x}{{\sqrt {4\alpha t}}}}\right)\right]\end{aligned}} In the last step, we make use of the fact that ∫ e − x 2 d x = π 2 erf ⁡ ( x ) . {\displaystyle \int e^{-x^{2}}\mathrm {d} x={\frac {\sqrt {\pi }}{2}}\operatorname {erf} (x).} \int e^{{-x^{{2}}}}{\mathrm {d}}x={\frac {{\sqrt {\pi }}}{2}}\operatorname {erf}(x). A plot of this function over time above shows that the "sharpness" of the function diminishes over time, eventually tending towards an equilibrium solution. This is what the heat equation is supposed to do - it says that the time rate of change of u ( x , t ) {\displaystyle u(x,t)} u(x,t) is proportional to the curvature of u ( x , t ) , {\displaystyle u(x,t),} u(x,t), as denoted by the spatial second derivative, so quantities obeying the heat equation will tend to smooth themselves out over time. The steady-state solution where ∂ u ∂ t = 0 {\displaystyle {\frac {\partial u}{\partial t}}=0} {\frac {\partial u}{\partial t}}=0 will therefore obey Laplace's equation. Setting α = 1 , {\displaystyle \alpha =1,} \alpha =1, the initial conditions are plotted in blue, while u ( x , t ) {\displaystyle u(x,t)} u(x,t) is being plotted for values t = 0.005 , {\displaystyle t=0.005,} t=0.005, t = 0.1 , {\displaystyle t=0.1,} t=0.1, and t = 0.3 , {\displaystyle t=0.3,} t=0.3, for orange, green, and red plots, respectively.

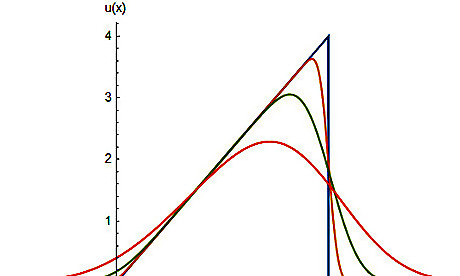
Find u ( x , t ) {\displaystyle u(x,t)} u(x,t) given initial conditions of the ramp function over a restricted domain. Specifically, u 0 ( x ) = x ( Θ ( x ) − Θ ( x − 4 ) ) , {\displaystyle u_{0}(x)=x(\Theta (x)-\Theta (x-4)),} u_{{0}}(x)=x(\Theta (x)-\Theta (x-4)), where Θ ( x ) {\displaystyle \Theta (x)} \Theta (x) denotes the Heaviside step function. This is the ramp function over the domain [ 0 , 4 ] . {\displaystyle [0,4].} [0,4]. Its solution is slightly more complicated. To find u ( x , t ) , {\displaystyle u(x,t),} u(x,t), we need to split the integral into two pieces. u ( x , t ) = 1 4 π α t ∫ − ∞ ∞ y ( Θ ( y ) − Θ ( y − 4 ) ) e − ( x − y ) 2 / 4 α t d y = 1 4 π α t ∫ 0 ∞ y e − ( x − y ) 2 / 4 α t d y − 1 4 π α t ∫ 4 ∞ y e − ( x − y ) 2 / 4 α t d y {\displaystyle {\begin{aligned}u(x,t)&={\frac {1}{\sqrt {4\pi \alpha t}}}\int _{-\infty }^{\infty }y(\Theta (y)-\Theta (y-4))e^{-(x-y)^{2}/4\alpha t}\mathrm {d} y\\&={\frac {1}{\sqrt {4\pi \alpha t}}}\int _{0}^{\infty }ye^{-(x-y)^{2}/4\alpha t}\mathrm {d} y-{\frac {1}{\sqrt {4\pi \alpha t}}}\int _{4}^{\infty }ye^{-(x-y)^{2}/4\alpha t}\mathrm {d} y\end{aligned}}} {\begin{aligned}u(x,t)&={\frac {1}{{\sqrt {4\pi \alpha t}}}}\int _{{-\infty }}^{{\infty }}y(\Theta (y)-\Theta (y-4))e^{{-(x-y)^{{2}}/4\alpha t}}{\mathrm {d}}y\\&={\frac {1}{{\sqrt {4\pi \alpha t}}}}\int _{{0}}^{{\infty }}ye^{{-(x-y)^{{2}}/4\alpha t}}{\mathrm {d}}y-{\frac {1}{{\sqrt {4\pi \alpha t}}}}\int _{{4}}^{{\infty }}ye^{{-(x-y)^{{2}}/4\alpha t}}{\mathrm {d}}y\end{aligned}} We see that the second integral is different from the first only by the lower boundary. Therefore, we will only detail the process for the first integral only. We make a substitution which splits this integral into two integrals which we may easily evaluate. Note that u {\displaystyle u} u below refers to a substitution variable, not to the temperature density. ∫ 0 ∞ y e − ( x − y ) 2 / 4 α t d y = − 4 α t ∫ 0 ∞ ( x − y 4 α t ) e ( x − y 4 α t ) 2 d y + x ∫ 0 ∞ e − ( x − y 4 α t ) 2 d y = 4 α t ∫ x / 4 α t ∞ u e − u 2 d u − x 4 α t ∫ x / 4 α t − ∞ e − u 2 d u = 2 α t ∫ x 2 / 4 α t ∞ e − v d v − x π α t erf ⁡ ( u ) | x / 4 α t − ∞ = 2 α t e − x 2 / 4 α t + x π α t [ 1 + erf ⁡ ( x 4 α t ) ] {\displaystyle {\begin{aligned}\int _{0}^{\infty }ye^{-(x-y)^{2}/4\alpha t}\mathrm {d} y&=-{\sqrt {4\alpha t}}\int _{0}^{\infty }\left({\frac {x-y}{\sqrt {4\alpha t}}}\right)e^{\left({\frac {x-y}{\sqrt {4\alpha t}}}\right)^{2}}\mathrm {d} y+x\int _{0}^{\infty }e^{-\left({\frac {x-y}{\sqrt {4\alpha t}}}\right)^{2}}\mathrm {d} y\\&=4\alpha t\int _{x/{\sqrt {4\alpha t}}}^{\infty }ue^{-u^{2}}\mathrm {d} u-x{\sqrt {4\alpha t}}\int _{x/{\sqrt {4\alpha t}}}^{-\infty }e^{-u^{2}}\mathrm {d} u\\&=2\alpha t\int _{x^{2}/4\alpha t}^{\infty }e^{-v}\mathrm {d} v-x{\sqrt {\pi \alpha t}}\operatorname {erf} (u){\Bigg |}_{x/{\sqrt {4\alpha t}}}^{-\infty }\\&=2\alpha te^{-x^{2}/4\alpha t}+x{\sqrt {\pi \alpha t}}\left[1+\operatorname {erf} \left({\frac {x}{\sqrt {4\alpha t}}}\right)\right]\end{aligned}}} {\begin{aligned}\int _{{0}}^{{\infty }}ye^{{-(x-y)^{{2}}/4\alpha t}}{\mathrm {d}}y&=-{\sqrt {4\alpha t}}\int _{{0}}^{{\infty }}\left({\frac {x-y}{{\sqrt {4\alpha t}}}}\right)e^{{\left({\frac {x-y}{{\sqrt {4\alpha t}}}}\right)^{{2}}}}{\mathrm {d}}y+x\int _{{0}}^{{\infty }}e^{{-\left({\frac {x-y}{{\sqrt {4\alpha t}}}}\right)^{{2}}}}{\mathrm {d}}y\\&=4\alpha t\int _{{x/{\sqrt {4\alpha t}}}}^{{\infty }}ue^{{-u^{{2}}}}{\mathrm {d}}u-x{\sqrt {4\alpha t}}\int _{{x/{\sqrt {4\alpha t}}}}^{{-\infty }}e^{{-u^{{2}}}}{\mathrm {d}}u\\&=2\alpha t\int _{{x^{{2}}/4\alpha t}}^{{\infty }}e^{{-v}}{\mathrm {d}}v-x{\sqrt {\pi \alpha t}}\operatorname {erf}(u){\Bigg |}_{{x/{\sqrt {4\alpha t}}}}^{{-\infty }}\\&=2\alpha te^{{-x^{{2}}/4\alpha t}}+x{\sqrt {\pi \alpha t}}\left[1+\operatorname {erf}\left({\frac {x}{{\sqrt {4\alpha t}}}}\right)\right]\end{aligned}} The second integral is found by a similar process. − ∫ 4 ∞ y e − ( x − y ) 2 / 4 α t d y = − 2 α t e − ( x − 4 ) 2 / 4 α t − x π α t [ 1 + erf ⁡ ( x − 4 4 α t ) ] {\displaystyle -\int _{4}^{\infty }ye^{-(x-y)^{2}/4\alpha t}\mathrm {d} y=-2\alpha te^{-(x-4)^{2}/4\alpha t}-x{\sqrt {\pi \alpha t}}\left[1+\operatorname {erf} \left({\frac {x-4}{\sqrt {4\alpha t}}}\right)\right]} -\int _{{4}}^{{\infty }}ye^{{-(x-y)^{{2}}/4\alpha t}}{\mathrm {d}}y=-2\alpha te^{{-(x-4)^{{2}}/4\alpha t}}-x{\sqrt {\pi \alpha t}}\left[1+\operatorname {erf}\left({\frac {x-4}{{\sqrt {4\alpha t}}}}\right)\right] Hence, our final answer is written as follows. u ( x , t ) = α t π ( e − x 2 / 4 α t − e − ( x − 4 ) 2 / 4 α t ) + x 2 [ erf ⁡ ( x 4 α t ) − erf ⁡ ( x − 4 4 α t ) ] {\displaystyle {\begin{aligned}u(x,t)={\sqrt {\frac {\alpha t}{\pi }}}\left(e^{-x^{2}/4\alpha t}-e^{-(x-4)^{2}/4\alpha t}\right)+{\frac {x}{2}}\left[\operatorname {erf} \left({\frac {x}{\sqrt {4\alpha t}}}\right)-\operatorname {erf} \left({\frac {x-4}{\sqrt {4\alpha t}}}\right)\right]\end{aligned}}} {\begin{aligned}u(x,t)={\sqrt {{\frac {\alpha t}{\pi }}}}\left(e^{{-x^{{2}}/4\alpha t}}-e^{{-(x-4)^{{2}}/4\alpha t}}\right)+{\frac {x}{2}}\left[\operatorname {erf}\left({\frac {x}{{\sqrt {4\alpha t}}}}\right)-\operatorname {erf}\left({\frac {x-4}{{\sqrt {4\alpha t}}}}\right)\right]\end{aligned}} Setting α = 1 , {\displaystyle \alpha =1,} \alpha =1, the initial conditions are plotted in blue, while u ( x , t ) {\displaystyle u(x,t)} u(x,t) is being plotted for values t = 0.01 , {\displaystyle t=0.01,} t=0.01, t = 0.1 , {\displaystyle t=0.1,} t=0.1, and t = 0.5 , {\displaystyle t=0.5,} t=0.5, for orange, green, and red plots, respectively.