Finding the Factors of a Number: A Tutorial

• Factoring a number is when you simplify the number into smaller products (or factors) of the number.
• For example, 2 and 6 are factors of 12 because 2 × 6 equals 12.
• The easiest way to factor a number is to try and divide it by the smallest prime number, such as 2 or 3.

Factoring Basic Integers

Write your number. To begin factoring, all you need is a number. Any number will do, but for our purposes, let's start with a simple integer. Integers are numbers without fractional or decimal components (all positive and negative whole numbers are integers). For this example, let's use the number 12.

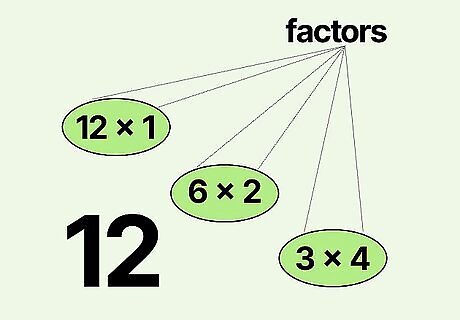
Find two more numbers that multiply to make your first number. Advanced Math Teacher Taylor Klein says that “The first way you can factor a number is by finding its factor pairs.” Any integer can be written as the product or result of two other integers. Thinking of a number as the result of two factors can require "backwards" thinking. You essentially must ask yourself, “What multiplication problem equals this number?” In our example, 12 has multiple factors: 12 × 1, 6 × 2, and 3 × 4 all equal 12. So, we can say that 12's factors are 1, 2, 3, 4, 6, and 12. Let’s work with the factors 6 and 2. Even numbers are especially easy to factor because every even number has 2 as a factor. 4 = 2 × 2, 26 = 13 × 2, etc.

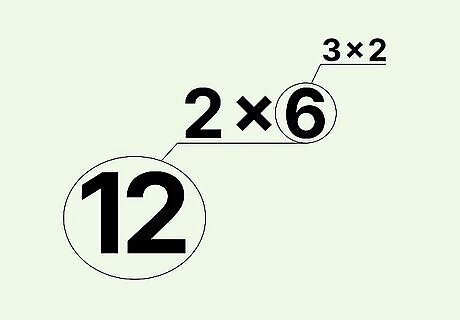
Determine whether any of your factors can be factored again. Lots of numbers—especially large ones—can be factored multiple times. When you've found two of a number's factors, if one has its own set of factors, you can also reduce this number to its factors. For instance, in our example, we have reduced 12 to 2 × 6. Notice that 6 has its own factors - 3 × 2 = 6. Thus, we can say that 12 = 2 × (3 × 2).

Stop factoring when you reach prime numbers. Prime numbers are numbers greater than 1 that are evenly divisible only by themselves and 1. For instance, 2, 3, 5, 7, 11, 13, and 17 are all prime numbers. Advanced Math Teacher Taylor Klein notes that when you've factored a number so it's the product of exclusively prime numbers, you can stop factoring. In our example, we've reduced 12 to 2 × (2 × 3). 2, 2, and 3 are all prime numbers. If we were to factor further, we'd have to factor to (2 × 1) × ((2 × 1)(3 × 1)), which isn't typically useful, so it's usually avoided.

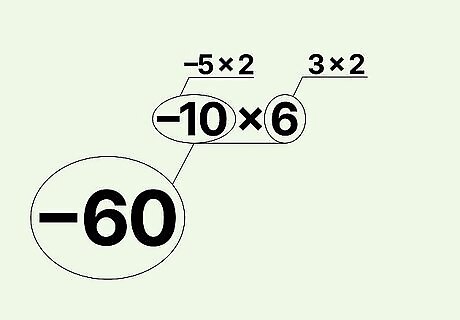
Factor negative numbers in the same way. Negative numbers can be factored nearly identically to how positive numbers are factored. The sole difference is that the factors must multiply together to make a negative number, so an odd number of the factors must be negative. For example, let's factor -60: -60 = -10 × 6 -60 = (-5 × 2) × 6 -60 = (-5 × 2) × (3 × 2) -60 = -5 × 2 × 3 × 2. Note that having an odd number of negative numbers besides one will give the same product. For example, -5 × 2 × -3 × -2 also equals 60.

Factoring Larger Numbers

Write your number above a 2-column table. If you’re working with a larger number that has 4 or 5 digits, try using a table to organize your work. Write your number above a t-shaped table with two columns. For the purpose of our example, let's choose a 4-digit number to factor: 6,552.

Divide your number by the smallest possible prime factor. Divide your number by the smallest prime factor (besides 1) that divides into it evenly with no remainder. Write the prime factor in the left column and write your answer across from it in the right column. As noted above, even numbers are easier to start factoring because their smallest prime factor will always be 2. Odd numbers, on the other hand, will have smallest prime factors that differ. In our example, since 6,552 is even, we know that 2 is its smallest prime factor. 6,552 ÷ 2 = 3,276. In the left column, we'll write 2, and in the right column, write 3,276.

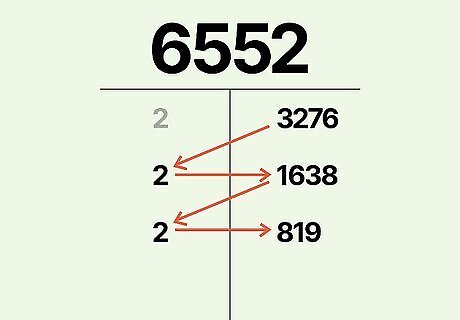
Continue dividing the number in the right column by its smallest prime factor. Repeat the previous step, but divide the newest number in the right column rather than dividing the number at the top of the table. Write the prime factor in the left column and the new number in the right column. Continue to repeat this process—with each repetition, the number in the right column should decrease. Let's continue with our process. 3,276 ÷ 2 = 1,638, so at the bottom of the left column, we'll write another 2, and at the bottom of the right column, we'll write 1,638. 1,638 ÷ 2 = 819, so we'll write 2 and 819 at the bottom of the two columns as before.

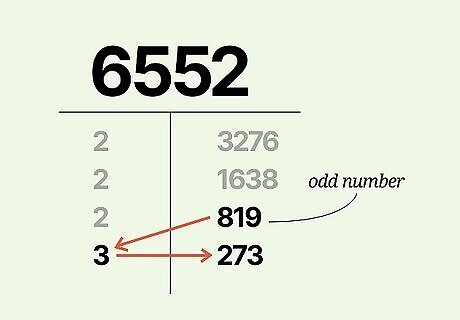
Deal with odd numbers by trying small prime factors. It’s more difficult to find the smallest prime factor of odd numbers because they don't automatically have 2 as their smallest prime factor. When you reach an odd number, try dividing by small prime numbers other than 2—such as 3, 5, 7, 11, and so on—until you find one that divides evenly with no remainder. This is the number's smallest prime factor. In our example, we've reached 819. 819 is odd, so 2 is not a factor of 819. Instead of writing down another 2, we'll try the next prime number: 3. 819 ÷ 3 = 273 with no remainder, so we'll write down 3 and 273. When guessing factors, try all prime numbers up to the square root of the largest factor found so far. If none of the factors you try up to this point divide evenly, you're probably trying to factor a prime number and have solved the problem.

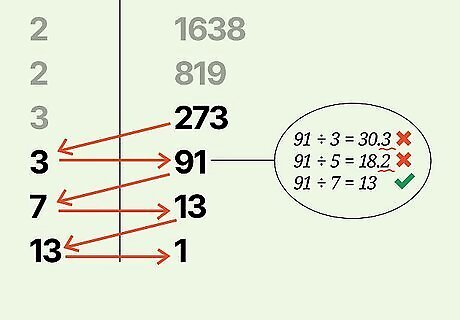
Continue until you reach 1. Continue dividing the numbers in the right column by their smallest prime factor until you obtain a prime number in the right column. Divide this number by itself. This will put the number in the left column and "1" in the right column. Let's finish factoring our number. See below for a detailed breakdown: Divide by 3 again: 273 ÷ 3 = 91, no remainder, so we'll write down 3 and 91. Let's try 3 again: 91 doesn't have 3 as a factor, nor does it have the next lowest prime (5) as a factor, but 91 ÷ 7 = 13, with no remainder, so we'll write down 7 and 13. Let's try 7 again: 13 doesn't have 7 as a factor, or 11 (the next prime), but it does have itself as a factor: 13 ÷ 13 = 1. So, to finish our table, we'll write down 13 and 1. We can finally stop factoring.

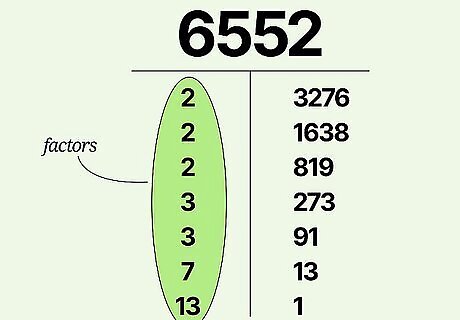
Use the numbers in the left-hand column as your original number's factors. Once you reach 1 in the right-hand column, you're done. The numbers listed on the left side of the table are your factors. In other words, when you multiply all these numbers together, the product will be the number at the top of the table. If the same factor appears multiple times, you can use exponent notation to save space. For instance, if your list of factors has four 2's, you can write 2 rather than 2 × 2 × 2 × 2. In our example 6,552 = 2 × 3 × 7 × 13. This is the complete factorization of 6,552 into prime numbers. No matter what order these numbers are multiplied in, the product will be 6,552.