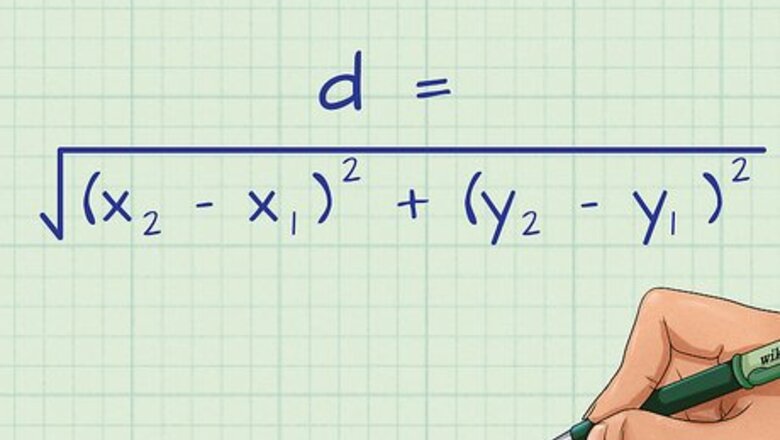
views
X
Research source
By using a basic geometric formula, measuring lines on a coordinate path becomes a relatively easy task.
Setting up the Formula
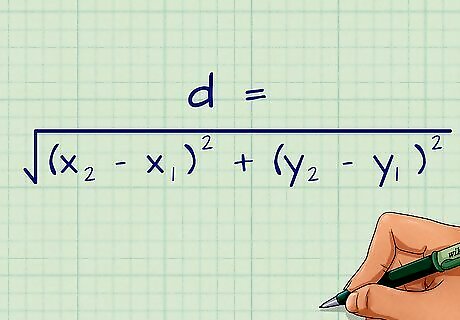
Set up the Distance Formula. The formula states that d = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 {\displaystyle d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}} d={\sqrt {(x_{{2}}-x_{{1}})^{{2}}+(y_{{2}}-y_{{1}})^{{2}}}}, where d {\displaystyle d} d equals the distance of the line, ( x 1 , y 1 ) {\displaystyle (x_{1},y_{1})} (x_{{1}},y_{{1}}) equal the coordinates of the first endpoint of the line segment, and ( x 2 , y 2 ) {\displaystyle (x_{2},y_{2})} (x_{{2}},y_{{2}}) equal the coordinates of the second endpoint of the line segment.
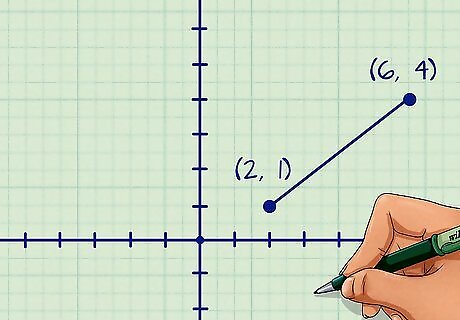
Find the coordinates of the line segment’s endpoints. These might already be given. If not, count along the x-axis and y-axis to find the coordinates. The x-axis is the horizontal axis; the y-axis is the vertical axis. The coordinates of a point are written as ( x , y ) {\displaystyle (x,y)} (x,y). For example, a line segment might have an endpoint at ( 2 , 1 ) {\displaystyle (2,1)} (2,1) and another at ( 6 , 4 ) {\displaystyle (6,4)} (6,4).
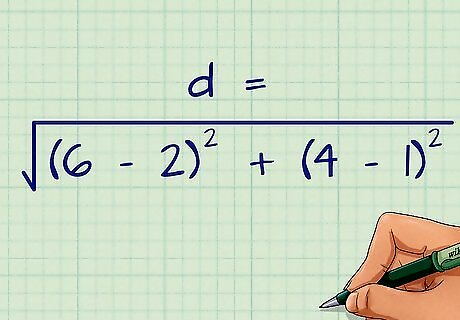
Plug the coordinates into the Distance Formula. Be careful to substitute the values for the correct variables. The two x {\displaystyle x} x coordinates should be inside the first set of parentheses, and the two y {\displaystyle y} y coordinates should be inside the second set of parentheses. For example, for points ( 2 , 1 ) {\displaystyle (2,1)} (2,1) and ( 6 , 4 ) {\displaystyle (6,4)} (6,4), your formula would look like this: d = ( 6 − 2 ) 2 + ( 4 − 1 ) 2 {\displaystyle d={\sqrt {(6-2)^{2}+(4-1)^{2}}}} d={\sqrt {(6-2)^{{2}}+(4-1)^{{2}}}}
Calculating the Distance
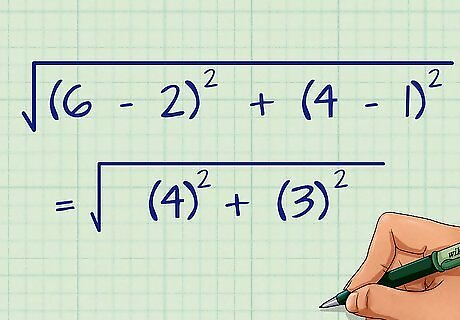
Calculate the subtraction in parentheses. By using the order of operations, any calculations in parentheses must be completed first. For example: d = ( 6 − 2 ) 2 + ( 4 − 1 ) 2 {\displaystyle d={\sqrt {(6-2)^{2}+(4-1)^{2}}}} d={\sqrt {(6-2)^{{2}}+(4-1)^{{2}}}} d = ( 4 ) 2 + ( 3 ) 2 {\displaystyle d={\sqrt {(4)^{2}+(3)^{2}}}} d={\sqrt {(4)^{{2}}+(3)^{{2}}}}
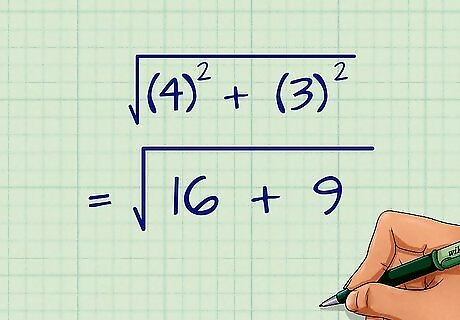
Square the value in parentheses. The order of operations states that exponents should be addressed next. For example: d = ( 4 ) 2 + ( 3 ) 2 {\displaystyle d={\sqrt {(4)^{2}+(3)^{2}}}} d={\sqrt {(4)^{{2}}+(3)^{{2}}}} d = 16 + 9 {\displaystyle d={\sqrt {16+9}}} d={\sqrt {16+9}}
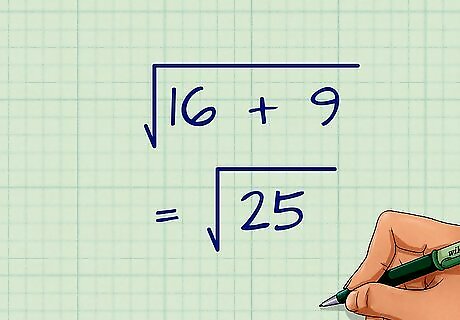
Add the numbers under the radical sign. You do this calculation as if you were working with whole numbers. For example: d = 16 + 9 {\displaystyle d={\sqrt {16+9}}} d={\sqrt {16+9}} d = 25 {\displaystyle d={\sqrt {25}}} d={\sqrt {25}}
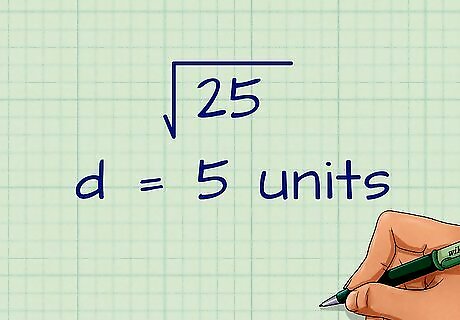
Solve for d {\displaystyle d} d. To reach your final answer, find the square root of the sum under the radical sign. Since you are finding a square root, you may have to round your answer. Since you are working on a coordinate plane, your answer will be in generic “units,” not in centimeters, meters, or another metric unit. For example: d = 25 {\displaystyle d={\sqrt {25}}} d={\sqrt {25}} d = 5 {\displaystyle d=5} d=5 units
















Comments
0 comment