views
Using Nilakantha Series
Understand the Nilakantha series. The Nilakantha series starts with: π = 3 + 4 2 ∗ 3 ∗ 4 − 4 4 ∗ 5 ∗ 6 + 4 6 ∗ 7 ∗ 8 − 4 8 ∗ 9 ∗ 10 . . . {\displaystyle \pi =3+{\frac {4}{2*3*4}}-{\frac {4}{4*5*6}}+{\frac {4}{6*7*8}}-{\frac {4}{8*9*10}}...} {\displaystyle \pi =3+{\frac {4}{2*3*4}}-{\frac {4}{4*5*6}}+{\frac {4}{6*7*8}}-{\frac {4}{8*9*10}}...}and continues according to this pattern. So the algorithm that you want to write is as follows: Begin with 3 as "answer", and a number n = 2 {\displaystyle n=2} n=2 Calculate 4 n ∗ ( n + 1 ) ∗ ( n + 2 ) {\displaystyle {\frac {4}{n*(n+1)*(n+2)}}} {\displaystyle {\frac {4}{n*(n+1)*(n+2)}}}. Add or subtract the result of that calculation from the answer. Repeat for a specified amount of times. Return and display the answer.
Create a new text file. You can use any IDE of your choice, or just a text editor. Give your file the extension .py so that your computer recognizes it as Python program file.
Import the decimal module. If you use Python without it or similar libraries, precision will be limited to 17 digits. This module, however, will allow you to have arbitrary precision for the digits. It is a default library of Python, so you do not need to install it separately. from decimal import *
Set the digit precision for Decimals. How big you make it depends on how many digits of π you want to calculate. For example, to calculate 100 digits of π, add the line: getContext().prec = 100
Define a function for the Nilakantha series. For programming, you can imagine that series as a function that takes the amount of iterations, calculates the series with that amount of iterations, and returns the approximation of π. In Python, the function will have the following structure: def nilakantha(reps): # Calculations will be here return answer
Set the starting values of the variables. answer is initially 3. Make sure to make it a Decimal, because it is the number for which you want the high precision provided by the decimal library. Also set a variable op to 1. That variable will be used later to alternate between addition and subtraction. def nilakantha(reps): answer = Decimal(3.0) op = 1 # Calculations will be here return answer
Add a for-loop. The for-loop will set a variable n to 2 initially. Then it will do what written is inside the loop and increment the value of n by 2, and repeat this process until the upper limit — 2*reps+1 — is reached. def nilakantha(reps): answer = Decimal(3.0) op = 1 for n in range(2, 2*reps+1, 2): # Calculations will be here return answer
Calculate an element of the Nilakantha series and add it to the answer. It is enough to make one part of the fraction a Decimal, Python will convert the other parts accordingly. Program the formula, but also multiply it with op. In the first cycle, op is set to 1, so multiplying with it does nothing. But it will be set to other values later. for n in range(2, 2*reps+1, 2): result += 4/Decimal(n*(n+1)*(n+2)*op)
Multiply op with -1. If op was 1, that will make it -1. If it was -1, that will make it 1. Adding a negative number is like subtracting a positive number. This is how the program alternates between addition and subtraction. for n in range(2, 2*reps+1, 2): result += 4/Decimal(n*(n+1)*(n+2)*op) op *= -1
Write an interface for the function. You will most likely want a way to input how many iterations of the series should be used, and a way to display the approximation of π that you calculated. print("How many repetitions?") repetitions = int(input()) print(nilakantha(repetitions)) If you haven't memorized many digits of π, you may also want to display the actual beginning of π to compare with your result. If that is the case, add the following line: print("3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679") (If you need more digits of π for your comparison, you can copy them from the internet.)
Check your code. Your entire code should now look like this (you can omit the last line): from decimal import * getcontext().prec = 100 def nilakantha(reps): result = Decimal(3.0) op = 1 n = 2 for n in range(2, 2*reps+1, 2): result += 4/Decimal(n*(n+1)*(n+2)*op) op *= -1 return result print("How many repetitions?") repetitions = int(input()) print(nilakantha(repetitions)) print("3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679")
Run your program. Click on the "Run" symbol of your IDE. In Python's IDLE, press F5. If you were working in a simple text editor, save your file, and run it with Python. Start with a small amount of iterations, like 100. This will let you see whether the program works. Be prepared to wait if you want many digits of π. For example, doing a million iterations of this series gives you 18 digits of π correctly, and it takes approximately 30 seconds.
Using Monte Carlo Method
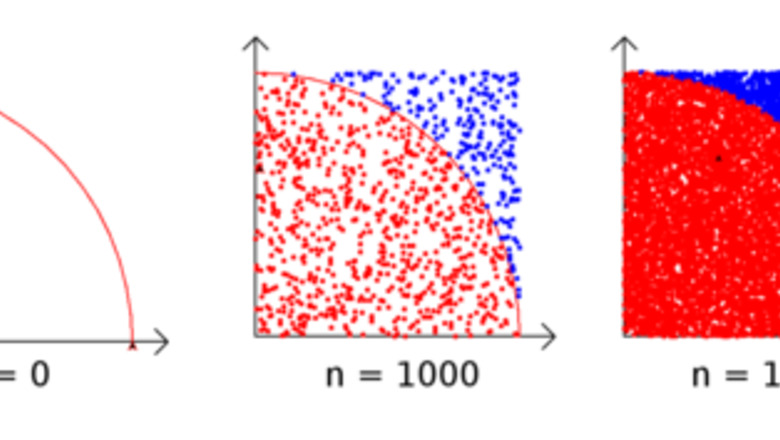
Understand the Monte-Carlo method. Imagine a square with any length, and inside it a quarter of a circle with a radius that is same as that length. The program will generate random points inside the square, and then check whether they are also inside the circle. With a lot of points, dividing the amount of points inside the quarter-circle by the amount of points inside the square will be like dividing the area of the quarter-circle by the area of the square. So, because of: A q u a r t e r c i r c l e A s q u a r e = 1 4 π r 2 r 2 = 1 4 π {\displaystyle {\frac {A_{quartercircle}}{A_{square}}}={\frac {{\frac {1}{4}}\pi r^{2}}{r^{2}}}={\frac {1}{4}}\pi } {\displaystyle {\frac {A_{quartercircle}}{A_{square}}}={\frac {{\frac {1}{4}}\pi r^{2}}{r^{2}}}={\frac {1}{4}}\pi }You can calculate π with: 4 A q u a r t e r c i r c l e A s q u a r e = π {\displaystyle 4{\frac {A_{quartercircle}}{A_{square}}}=\pi } {\displaystyle 4{\frac {A_{quartercircle}}{A_{square}}}=\pi } The program can't just use the area directly because calculating the area of the quarter-circle would require π, which this program is supposed to determine. This is not an efficient method. You will have to wait quite long to get the same amount of digits of π as, for example, the Nilakantha series. However, it is a method that is easy to imagine and visualize (at the cost of even slower performance).
Import the necessary modules. You don't need to install them, they all already come installed with Python. random has the function for generating random numbers. math provides some mathematical functions, like the square root, which you will need for calculating the distance of a point. turtle will draw what the program is doing. This will make it slower, but it can help understand the method and be interesting to watch for some time. If you want to calculate π fast, you should choose a different method anyway. import random import math import turtle
Ask the user about how many points to calculate. This can be with the following code: print("Insert number of points:") np = input() while not np.isdigit(): print("Insert number of points:") np = input() np = int(np)
Make the turtle faster. By default, the turtle is not as fast as it could be. Change this by setting the turtle's speed to fastest: turtle.speed("fastest")
Draw the situation. Draw the coordinate system in which the rectangle and the quarter-circle are, and draw the quarter-circle. First, define a variable that stores the length of the square and the radius of the quarter-circle in pixels (you only need one variable, because this is the same number). This will save you a lot of work if you decide to change the size of the quarter-circle and square. length = 300 # radius of circle and length of the square in pixels Then, you need to actually draw the coordinate axes and the circle. This code is long, but all it does is move the turtle around to draw these things. #draw y axis turtle.pensize(2) turtle.forward(length + 40) turtle.left(135) turtle.forward(20) turtle.back(20) turtle.left(90) turtle.forward(20) turtle.penup() turtle.home() turtle.pendown() #draw x axis turtle.left(90) turtle.forward(length + 40) turtle.left(135) turtle.forward(20) turtle.back(20) turtle.left(90) turtle.forward(20) turtle.penup() turtle.goto(0,length) turtle.left(45) turtle.left(180) turtle.pendown() #draw quarter of circle turtle.pencolor("red") turtle.circle(length,-90)
Make a loop for the calculations that you'll need to do for each dot. Before the loop, set the amount of dots inside the circle (the variable inside) to 0. inside = 0 for i in range(0,np):
Get a random position for the dot. You will need two random numbers — the x-position and the y-position of the dot. For easier calculations, we left the center of the quarter-circle at (0,0) in the previous steps. This means you need both numbers to be between 0 and the length of the square. Get such numbers with the random.uniform() function: #get dot position x = random.randint(0,length) y = random.randint(0,length)
Check whether the dot is inside the quarter-circle. You need to calculate the distance between the dot and the centre, and check whether it is less or equal to the radius of the quarter-circle. To calculate the distance, you need to use Pythagoras' theorem. It is: d = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 {\displaystyle d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}} {\displaystyle d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}}However, since the centre is located at (0,0), x1 and y1 are both 0 and can be ignored. The formula is simpler: d = x 2 2 + y 2 2 {\displaystyle d={\sqrt {{x_{2}}^{2}+{y_{2}}^{2}}}} {\displaystyle d={\sqrt {{x_{2}}^{2}+{y_{2}}^{2}}}}In Python code (x2 and y2 are the coordinates that you got in the previous step): #determine distance from center d = math.sqrt(x**2 + y**2) If the point is inside the circle, increase the variable that counts the points inside the circle by 1. For better overview, set the colour of a dot inside the circle to red and of a dot outside the circle to blue. if d <= length: inside += 1 turtle.pencolor("red") else: turtle.pencolor("blue")
Draw the dot. Use the turtle for this: #draw dot turtle.penup() turtle.goto(x,y) turtle.pendown() turtle.dot()
Display the results after the loop finishes. Tell the user how many points were inside the circle, and which value of π this calculation gave: print("Inside of quarter-circle:") print(inside) print("Total amount of points:") print(np) print("Pi is approximately:") print((inside / np) * 4.0)
Exit only when the user clicks on the screen. This is done with the exitonclick() function of the turtle module. Otherwise, the window with the drawing would close when the calculations finish, and the user wouldn't have time to look at it. Add the line: turtle.exitonclick()
Check your code. Your entire code now should be: import random import math import turtle print("Insert number of points:") np = input() while not np.isdigit(): print("Insert number of points:") np = input() np = int(np) turtle.speed("fastest") length = 300 # radius of circle and length of the square in pixels #draw y axis turtle.pensize(2) turtle.forward(length + 40) turtle.left(135) turtle.forward(20) turtle.back(20) turtle.left(90) turtle.forward(20) turtle.penup() turtle.home() turtle.pendown() #draw x axis turtle.left(90) turtle.forward(length + 40) turtle.left(135) turtle.forward(20) turtle.back(20) turtle.left(90) turtle.forward(20) turtle.penup() turtle.goto(0,length) turtle.left(45) turtle.left(180) turtle.pendown() #draw quarter of circle turtle.pencolor("red") turtle.circle(length,-90) inside = 0 for i in range(0,np): #get dot position x = random.uniform(0,length) y = random.uniform(0,length) #determine distance from center d = math.sqrt(x**2 + y**2) if d <= length: inside += 1 turtle.pencolor("red") else: turtle.pencolor("blue") #draw dot turtle.penup() turtle.goto(x,y) turtle.pendown() turtle.dot() print("Inside of quarter-circle:") print(inside) print("Total amount of points:") print(np) print("Pi is approximately:") print((inside / np) * 4.0) turtle.exitonclick()
Run your program. Click on the "Run" symbol of your IDE. In Python's IDLE, press F5. If you were working in a simple text editor, save your file, and run it with Python. Start with a small amount of dots, like 100. This will let you see whether the program works. Be prepared to wait very long. Even calculating 1000 points takes approx. 1½ minutes, and gives a few (1–2) digits of π. Calculating 10000 points takes 15 minutes, and gives 2–3 digits of π.

















Comments
0 comment